
【题目】已知 f(x)= ![]() sin2x﹣2sin2x,
sin2x﹣2sin2x,
(1)求f(x)的最小正周期和单调递减区间;
(2)若x∈[﹣ ![]() ,
, ![]() ],求f(x)的最大值及取得最大值时对应的x的取值.
],求f(x)的最大值及取得最大值时对应的x的取值.
【答案】
(1)解:因为 f(x)= ![]() sin2x﹣2sin2x=
sin2x﹣2sin2x= ![]() sin2x+cos2x﹣1=2sin(2x+
sin2x+cos2x﹣1=2sin(2x+ ![]() )﹣1,
)﹣1,
所以,函数的周期为T= ![]() =π,即函数f(x)的最小正周期为 π.
=π,即函数f(x)的最小正周期为 π.
令 2kπ+ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈z,解得 kπ+
,k∈z,解得 kπ+ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,k∈z,
,k∈z,
所以f(x)的单调递减区间为[kπ+ ![]() ,kπ+
,kπ+ ![]() ]
]
(2)解:因为﹣ ![]() ≤x≤
≤x≤ ![]() ,得﹣
,得﹣ ![]() ≤2x+
≤2x+ ![]() ≤
≤ ![]() ,∴﹣
,∴﹣ ![]() ≤sin(2x+
≤sin(2x+ ![]() )≤1.
)≤1.
∴﹣2≤2sin(2x+ ![]() )﹣1≤1,
)﹣1≤1,
所以,函数f(x)的最大值为1.
此时,2x+ ![]() =
= ![]() ,即 x=
,即 x= ![]()
【解析】(1)利用三角函数的恒等变换化简函数f(x)的解析式为2sin(2x+ ![]() )﹣1,由此求得函数的周期,令2kπ+
)﹣1,由此求得函数的周期,令2kπ+ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈z,解得x的范围,可得f(x)的单调递减区间.(2)根据﹣
,k∈z,解得x的范围,可得f(x)的单调递减区间.(2)根据﹣ ![]() ≤x≤
≤x≤ ![]() ,求得2x+
,求得2x+ ![]() 的范围,可得sin(2x+
的范围,可得sin(2x+ ![]() )﹣1的范围,即为函数的值域,从而求得函数的最大值.
)﹣1的范围,即为函数的值域,从而求得函数的最大值.
【考点精析】本题主要考查了三角函数的最值的相关知识点,需要掌握函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】凸四边形PABQ中,其中A,B为定点,AB= ![]() ,P,Q为动点,满足AP=PQ=QB=1.
,P,Q为动点,满足AP=PQ=QB=1.
(1)写出cosA与cosQ的关系式;
(2)设△APB和△PQB的面积分别为S和T,求S2+T2的最大值,以及此时凸四边形PABQ的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为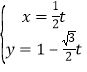 (t为参数
(t为参数![]() 以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆C的极坐标方程为
以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆C的极坐标方程为![]() .
.
![]() Ⅰ
Ⅰ![]() 判断直线l与圆C的交点个数;
判断直线l与圆C的交点个数;
![]() Ⅱ
Ⅱ![]() 若圆C与直线l交于A,B两点,求线段AB的长度.
若圆C与直线l交于A,B两点,求线段AB的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 满足
满足![]() ,且
,且![]() 的最小值是
的最小值是![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有唯一实数根,求实数
上有唯一实数根,求实数![]() 的取值范围;
的取值范围;
(3)函数![]() ,对任意
,对任意![]() 都有
都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,矩形
的中点,矩形![]() 所在的平面和平面
所在的平面和平面![]() 互相垂直.
互相垂直.
(![]() )求证:
)求证:![]() 平面
平面![]() .
.
(![]() )设
)设![]() 的中点为
的中点为![]() ,求证:
,求证:![]() 平面
平面![]() .
.
(![]() )求三棱锥
)求三棱锥![]() 的体积.(只写出结果,不要求计算过程)
的体积.(只写出结果,不要求计算过程)
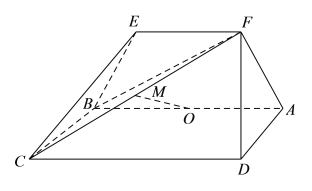
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知t为实数,函数![]() ,其中
,其中![]()
(1)若![]() ,求
,求![]() 的取值范围。
的取值范围。
(2)当![]() 时,
时,![]() 的图象始终在
的图象始终在![]() 的图象的下方,求t的取值范围;
的图象的下方,求t的取值范围;
(3)设![]() ,当
,当![]() 时,函数
时,函数![]() 的值域为
的值域为![]() ,若
,若![]() 的最小值为
的最小值为![]() ,求实数a的值.
,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图甲所示,放在水平地面上的物体,受到方向不变的水平推力F的作用,F的大小与时间t的关系和物体运动速度v与时间t的关系如图乙所示.下列判断正确的是:
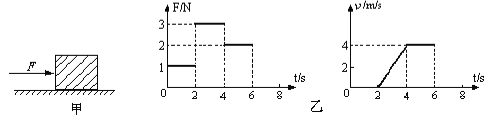
A.t=3s时,物体受到力的合力为零
B.t=6s时,将F撤掉,物体立刻静止
C.2s~4s内物体所受摩擦力逐渐增大
D.t=1s时,物体所受摩擦力是1N
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种商品在![]() 天内每件的销售价格
天内每件的销售价格![]() (元)与时间
(元)与时间![]() (
(![]() )(天)的函数关系满足函数
)(天)的函数关系满足函数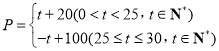 ,该商品在
,该商品在![]() 天内日销售量
天内日销售量![]() (件)与时间
(件)与时间![]() (
(![]() )(天)之间满足一次函数关系如下表:
)(天)之间满足一次函数关系如下表:
第 |
|
|
|
|
|
|
|
|
|
(1)根据表中提供的数据,确定日销售量![]() 与时间
与时间![]() 的一次函数关系式;
的一次函数关系式;
(2)求该商品的日销售金额的最大值并指出日销售金额最大的一天是![]() 天中的第几天,(日销售金额
天中的第几天,(日销售金额![]() 每件的销售价格
每件的销售价格![]() 日销售量)
日销售量)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com