

图3-3-2
(1)投中大圆内的概率是多少?
(2)投中小圆与中圆形成的圆环的概率是多少?
(3)投中大圆之外的概率是多少?
思路分析:投中正方形木板上每一点(投中线上或没投中都不算)都是一个基本事件,这一点可以是正方形木板上任意一点,因而基本事件有无限多个,且每个基本事件发生的可能性是相等的,所以投中某一部分的概率只与这部分的几何度量(面积)有关,这符合几何概型的条件.
解:记A={投镖投中大圆内},B={投镖投中小圆与中圆形成的圆环},C={投镖投中大圆之外},S正方形=162=256(cm2),S大圆=π×62=36π(cm2),S中圆=π×42=16π(cm2),S小圆=π×22=4π(cm2).
所以(1)P(A)=![]() ;
;
(2)P(B)=![]() ;
;
(3)P(C)=![]() .
.
所以,(1)投中大圆内的概率是![]() ;
;
(2)投中小圆与中圆形成的圆环的概率是![]() ;
;
(3)投中大圆之外的概率是1-![]() .
.
巧解提示 要准确把握图形的边界与基本事件所表示的区域的关系.如本题,投中线上或投不中都不算,因而投中正方形内各部分的任何一点都是等可能的.


科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:江苏省淮安五校2010-2011学年高一上学期期末考试数学试题 题型:044
围建一个面积为360 m2的矩形场地,要求矩形场地的一面利用旧墙(利用的旧墙需维修),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽度为2 m的进出口,如图所示已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙长度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元)

(1)将y表示为x的函数;
(2)写出f(x)的单调区间,并证明;
(3)根据(2),试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
查看答案和解析>>
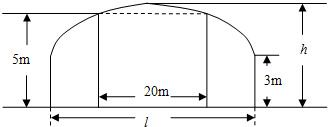
科目:高中数学 来源:2012-2013学年湖南省长沙市浏阳一中高二(上)第三次段考数学试卷(理科)(解析版) 题型:解答题
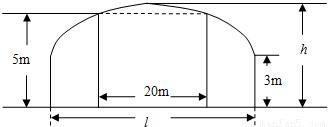
 +
+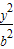 =1的面积公式为S=πab,柱体体积为底面积乘以高.)
=1的面积公式为S=πab,柱体体积为底面积乘以高.)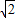 倍,试确定M、N的位置以及h的值,使总造价最少.
倍,试确定M、N的位置以及h的值,使总造价最少.查看答案和解析>>
科目:高中数学 来源:2009年湖南省长沙一中高考数学三模试卷(理科)(解析版) 题型:解答题
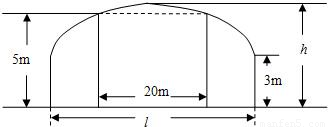
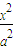 +
+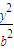 =1的面积公式为S=πab,柱体体积为底面积乘以高.)
=1的面积公式为S=πab,柱体体积为底面积乘以高.)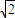 倍,试确定M、N的位置以及h的值,使总造价最少.
倍,试确定M、N的位置以及h的值,使总造价最少.查看答案和解析>>
科目:高中数学 来源:2010年重庆市部分重点中学高高考数学一模试卷(理科)(解析版) 题型:解答题
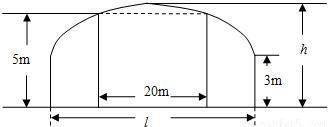
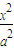 +
+ =1的面积公式为S=πab,柱体体积为底面积乘以高.)
=1的面积公式为S=πab,柱体体积为底面积乘以高.)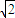 倍,试确定M、N的位置以及h的值,使总造价最少.
倍,试确定M、N的位置以及h的值,使总造价最少.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com