已知函数f(x)=|x2-1|+x2+kx,且定义域为(0,2).
(1)求关于x的方程f(x)=kx+3在(0,2)上的解;
(2)若f(x)是定义域(0,2)上的单调函数,求实数k的取值范围;
(3)若关于x的方程f(x)=0在(0,2)上有两个不同的解x1,x2,求k的取值范围.
【答案】
分析:(1)对x分0<x≤1与1<x<2两种情况讨论,使函数f(x)=|x
2-1|+x
2+kx中的绝对值符号去掉,从而可求得f(x)=kx+3在(0,2)上的解;
(2)将f(x)=|x
2-1|+x
2+kx化为:f(x)=|
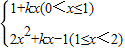
,对k与二次函数的对称轴分
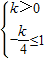
与
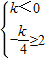
两种情况讨论,都可满足f(x)是定义域(0,2)上的单调函数,从而求得k的取值范围;
(3)解法一:当0<x≤1时,kx=-1,①,当1<x<2时,2x
2+kx-1=0,②
对于①②再分k=0与k≠0讨论解决;
解法二:f(x)=0⇒)=|x
2-1|+x
2=-kx,|x
2-1|+x
2=
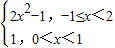
,从而-k=
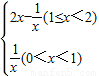
,
再分析函数的单调情况及取值,从而得到答案.
解答:解:(1)∵f(x)=|x
2-1|+x
2+kx,
∴f(x)=kx+3即|x
2-1|+x
2=3
当0<x≤1时,|x
2-1|+x
2=1-x
2+x
2=1,此时该方程无解…(1分)
当1<x<2时,|x
2-1|+x
2=2x
2-1,原方程等价于:x
2=2,此时该方程的解为
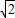
.
综上可知:方程f(x)=kx+3在(0,2)上的解为
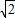
.…(3分)
(2)∵f(x)=|x
2-1|+x
2+kx,
∴f(x)=
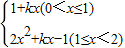
…(4分)
∵k×1+1=2×1+k-1,…(5分)
可得:若f(x)是单调递增函数,则
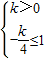
∴此时k>0…(6分)
若f(x)是单调递减函数,则
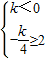
∴此时k≤-8,…(7分)
综上可知:f(x)是单调函数时k的取值范围为(-∞,-8]∪(0,+∞).…(8分)
(2)[解法一]:当0<x≤1时,kx=-1,①
当1<x<2时,2x
2+kx-1=0,②
若k=0则①无解,②的解为x=±
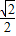
∉(1,2)故k=0不合题意 …(9分)
若k≠0则①的解为x=-
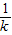
,
(Ⅰ)当-
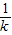
∈(0,1]时,k≤-1时,方程②中△=k
2+8>0,
故方程②中一根在(1,2)内另一根不在(1,2)内,…(10分)
设g(x)=2x
2+kx-1,而x
1x
2=-

<0则
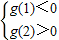
,
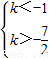
又k≤-1,
故-

<k<-1,…(11分)
(Ⅱ)当-
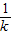
∉(0,1]时,即-1<k<0或k>0时,方程②在(1,2)须有两个不同解,…12分
而x
1x
2=-

<0,知道方程②必有负根,不合题意…13分
综上所述,故-

<k<-1,…14分.
解法二:f(x)=0⇒)=|x
2-1|+x
2=-kx,…9分
|x
2-1|+x
2=
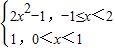
,…10分
∴-k=
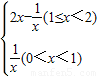
…12分
分析函数的单调情况及取值情况易得解,用图象法须作图,再用必要文字说明…13分
利用分段函数的图象得:-

<k<-1,…14分
点评:本题考查带绝对值的函数,解决的关键是通过分类讨论去绝对值符号,难点在于复杂的讨论与转化,考查学生综合分析与运算的能力,考查化归思想,分类讨论思想、属性结合思想,属于难题.

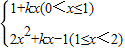 ,对k与二次函数的对称轴分
,对k与二次函数的对称轴分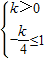 与
与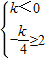 两种情况讨论,都可满足f(x)是定义域(0,2)上的单调函数,从而求得k的取值范围;
两种情况讨论,都可满足f(x)是定义域(0,2)上的单调函数,从而求得k的取值范围;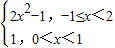 ,从而-k=
,从而-k=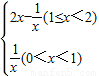 ,
,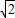 .
.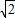 .…(3分)
.…(3分)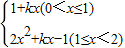 …(4分)
…(4分)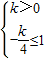
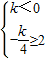
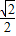 ∉(1,2)故k=0不合题意 …(9分)
∉(1,2)故k=0不合题意 …(9分)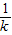 ,
,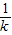 ∈(0,1]时,k≤-1时,方程②中△=k2+8>0,
∈(0,1]时,k≤-1时,方程②中△=k2+8>0, <0则
<0则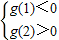 ,
,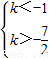 又k≤-1,
又k≤-1, <k<-1,…(11分)
<k<-1,…(11分)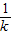 ∉(0,1]时,即-1<k<0或k>0时,方程②在(1,2)须有两个不同解,…12分
∉(0,1]时,即-1<k<0或k>0时,方程②在(1,2)须有两个不同解,…12分 <0,知道方程②必有负根,不合题意…13分
<0,知道方程②必有负根,不合题意…13分 <k<-1,…14分.
<k<-1,…14分.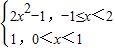 ,…10分
,…10分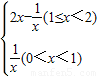 …12分
…12分 <k<-1,…14分
<k<-1,…14分

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案