
若实数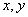 满足
满足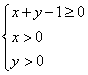 ,则
,则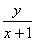 的取值范围是( )
的取值范围是( )
A.(0,2) B.(0,2) C.(2,+∞) D.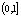
科目:高中数学 来源: 题型:
某运输公司有12名驾驶员和19名工人,有8辆载重量为10吨的甲型卡车和7辆载重量为6吨的乙型卡车.某天需运往 地至少72吨的货物,派用的每辆车需满载且只运送一次.派用的每辆甲型卡车需配2名工人,运送一次可得利润450元;派用的每辆乙型卡车需配1名工人,运送一次可得利润350元.该公司合理计划当天派用两类卡车的车辆数,可得最大利润z=( )
地至少72吨的货物,派用的每辆车需满载且只运送一次.派用的每辆甲型卡车需配2名工人,运送一次可得利润450元;派用的每辆乙型卡车需配1名工人,运送一次可得利润350元.该公司合理计划当天派用两类卡车的车辆数,可得最大利润z=( )
A.4650元 B.4700元 C.4900元 D.5000元
查看答案和解析>>
科目:高中数学 来源: 题型:
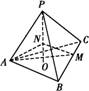
如图,三棱锥P ABC的高PO=8,AC=BC=3,
ABC的高PO=8,AC=BC=3,
∠ACB=30°,M,N分别在BC和PO上,且CM=x,PN=2CM,则三棱锥N AMC的体积V在x∈(0,3]上的最大体积是 .
AMC的体积V在x∈(0,3]上的最大体积是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com