
 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源:不详 题型:解答题
 建,必须在建完前一期工程后再建后一期工程。已知甲公司获得第一期、第二期、第三期工程承包权的概率分别为
建,必须在建完前一期工程后再建后一期工程。已知甲公司获得第一期、第二期、第三期工程承包权的概率分别为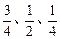 .
.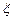 的分布列和数学期望
的分布列和数学期望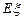 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 三口就如何将手中的10万块钱投资理财,提出了二种方案:第一种方案:将10万块钱全部用来买股,据分析预测:投资股市一年可能获利40%,也可能亏损20%(只有这两种可能),且获利的概率为
三口就如何将手中的10万块钱投资理财,提出了二种方案:第一种方案:将10万块钱全部用来买股,据分析预测:投资股市一年可能获利40%,也可能亏损20%(只有这两种可能),且获利的概率为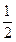 .第二种方案:将10万年钱全部用来买基金,据分析预测:投资基金一年可能获利20%,也可以损失10%,也可以不赔不赚,且三种情况发生的概率分别为
.第二种方案:将10万年钱全部用来买基金,据分析预测:投资基金一年可能获利20%,也可以损失10%,也可以不赔不赚,且三种情况发生的概率分别为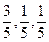 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
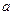 ,第二次出现的点数为
,第二次出现的点数为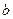 ,设复数
,设复数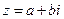 .
.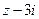 ”为实数”的概率;
”为实数”的概率;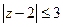 ”的概率.
”的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
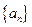 中,
中,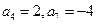 。现从
。现从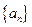 中的前10项中随机取数,每次取出一个数,取后放回,连续抽取3次,假定每次取数互不影响,那么在这三次取数中
中的前10项中随机取数,每次取出一个数,取后放回,连续抽取3次,假定每次取数互不影响,那么在这三次取数中 ,取出的数恰好为两个正数一个负数的概率为_________(用数字作答)
,取出的数恰好为两个正数一个负数的概率为_________(用数字作答)查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
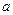 ,第二次出现的点数为
,第二次出现的点数为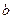 .若事件“点
.若事件“点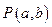 落在直线
落在直线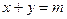 (
(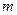 为常数)上”的概率最大,则
为常数)上”的概率最大,则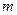 =" " ▲ .
=" " ▲ .查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
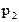 ,第3次取到合格品的概率是
,第3次取到合格品的概率是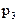 ,则 ( )
,则 ( )A. > > | B. = = | C. < < | D.不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com