
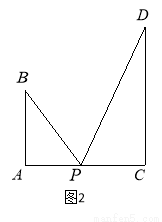
图1是某斜拉式大桥图片,为了了解桥的一些结构情况,学校数学兴趣小组将大桥的结构进行了简化,取其部分可抽象成图2所示的模型,其中桥塔 、
、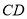 与桥面
与桥面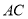 垂直,通过测量得知
垂直,通过测量得知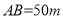 ,
,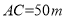 ,当
,当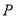 为
为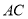 中点时,
中点时,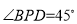 .
.
(1)求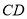 的长;
的长;
(2)试问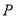 在线段
在线段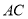 的何处时,
的何处时,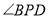 达到最大.
达到最大.


科目:高中数学 来源:2013-2014学年江苏省苏、锡、常、镇四市高三教学情况调查(一)文科数学试卷(解析版) 题型:解答题
已知函数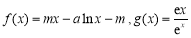 ,其中m,a均为实数.
,其中m,a均为实数.
(1)求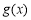 的极值;
的极值;
(2)设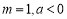 ,若对任意的
,若对任意的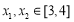
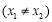 ,
, 恒成立,求
恒成立,求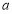 的最小值;
的最小值;
(3)设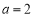 ,若对任意给定的
,若对任意给定的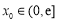 ,在区间
,在区间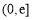 上总存在
上总存在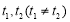 ,使得
,使得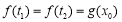 成立,求
成立,求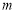 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省盐城市高三第三次模拟考试数学试卷(解析版) 题型:解答题
已知直线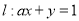 在矩阵
在矩阵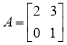 对应的变换作用下变为直线
对应的变换作用下变为直线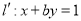 .
.
(1)求实数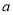 ,
,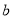 的值;
的值;
(2)若点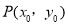 在直线
在直线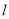 上,且
上,且 ,求点
,求点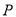 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省盐城市高三第三次模拟考试数学试卷(解析版) 题型:填空题
设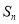 为数列
为数列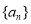 的前
的前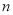 项和,
项和,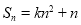 ,
,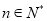 ,其中
,其中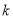 是常数.若对于任意的
是常数.若对于任意的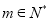 ,
,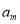 ,
,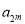 ,
,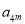 成等比数列,则
成等比数列,则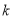 的值为 .
的值为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省盐城市高三第三次模拟考试数学试卷(解析版) 题型:填空题
某工厂甲、乙、丙三个车间生产同一产品,数量分别为120件,90件,60
件. 为了解它们的产品质量是否有显著差异,用分层抽样方法抽取了一个容量
为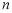 的样本进行调查,其中从丙车间的产品中抽取了4件,则
的样本进行调查,其中从丙车间的产品中抽取了4件,则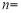 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省淮安市高三5月信息卷理科数学试卷(解析版) 题型:填空题
已知数列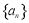 是各项均不为
是各项均不为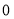 的等差数列,
的等差数列,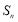 为其前
为其前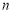 项和,且满足
项和,且满足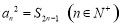 .若不等式
.若不等式 对任意的
对任意的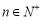 恒成立,则实数
恒成立,则实数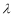 的最大值为 .
的最大值为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省淮安市高三Ⅲ级部决战四统测二理科数学试卷(解析版) 题型:填空题
若关于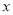 的不等式
的不等式 的解集中有且仅有4个整数解,则实数
的解集中有且仅有4个整数解,则实数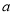 的取值范围是 .
的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com