
 ,则β=________.
,则β=________.
 利用差的正切函数公式化简,代入tanα求出tanβ的值,然后利用特殊角的函数值求出β即可.
利用差的正切函数公式化简,代入tanα求出tanβ的值,然后利用特殊角的函数值求出β即可. ;
;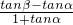 =
=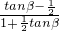 =
= ,解出tanβ=1,因为β为锐角,则β=
,解出tanβ=1,因为β为锐角,则β=



科目:高中数学 来源:2010-2011学年上海市外国语大学附中高一(下)期末数学试卷(解析版) 题型:选择题
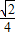
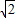
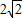
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com