
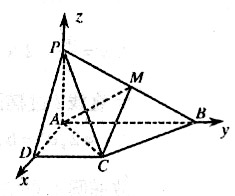
(08年德州市质检理)(12分) 已知四棱锥P―ABCD的底面为直角梯形,AB∥DC,∠DAB=900。,PA⊥底面ABCD且PA=AD=DC=1,AB=2,M是PB的中点
(1)证明:面PAD⊥面PCD;
(2)求AC与PB所成的角;
(3)求面AMC与面BMC所成二面角的大小

解析:以A为坐标原点AD长为单位长度,如图建立空间直角坐标系,则各点坐标为A(0,0,0),B(0,2,0),C(1,1,0),D(1,0,0),P(0,0,1),M(0,1,1/2),
(1)因![]() =(0,0,1),
=(0,0,1),![]() =(0,1,0),
=(0,1,0),
故![]() ,所以AP⊥DC.
,所以AP⊥DC.
由题设知AD⊥DC,且AP与AD是平面PAD内的两条相交直线,
由此得DC⊥面PAD.
又DC在面PCD上,故面PAD⊥面PCD 4分
(2)因![]() =(1,1,0),
=(1,1,0),![]() =(0,2,-1),
=(0,2,-1),
故![]()
所以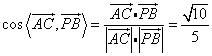
AC与PB所成的角为![]() 8分
8分
(3)由![]() =(0,1,1/2),
=(0,1,1/2),![]() =(1,0,一1/2),
=(1,0,一1/2),![]() =(一1,1,0)
=(一1,1,0)
设平面AMC与面BMC的法向量分别为![]() =(x,y,z),
=(x,y,z),![]() =(p,q,v),
=(p,q,v),
则![]() 解得:
解得:![]() =(1,一1,2),
=(1,一1,2),
同理![]() =(1,1,2),
=(1,1,2),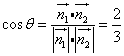
由题可知,二面角的平面角为钝角,
所以面AMC与面BMC二面角的大小![]() 12分
12分


科目:高中数学 来源: 题型:
(08年德州市质检理)(12分)甲有一只放有![]() 个红球,y个黄球,
个红球,y个黄球,![]() 个白球的箱子,且
个白球的箱子,且![]() (
(![]() 、
、![]() 、
、![]() ∈
∈![]() ),乙有一只放有3个红球,2个黄球,1个白球的箱子,两人各自从自己的箱子中任取一球,规定:当两球同色时甲胜,异色时乙胜
),乙有一只放有3个红球,2个黄球,1个白球的箱子,两人各自从自己的箱子中任取一球,规定:当两球同色时甲胜,异色时乙胜
(1)用![]() ,
,![]() ,
,![]() 表示甲胜的概率;
表示甲胜的概率;
(2)若又规定为甲取红、黄、白球而胜的得分分别为1、2、3分,否则得0分,求甲得分的期望的最大值及此时![]() ,
, ![]() ,
, ![]() 的值
的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com