
从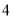 名男生和
名男生和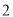 名女生中任选
名女生中任选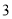 人参加演讲比赛,
人参加演讲比赛,
①求所选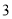 人都是男生的概率;
人都是男生的概率;
②求所选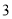 人恰有
人恰有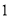 名女生的概率;
名女生的概率;
③求所选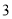 人中至少有
人中至少有 名女生的概率。
名女生的概率。
(1) ;(2)
;(2) ;(3)
;(3) .
.
【解析】
试题分析:(1)首先列出所有的情况,所有的选法共有20 种,其中,所选3人都是男生的选法有4种,由此求得所选3人都是男生的概率.(2)所选3人恰有1名女生的选法有12 种,所有的选法共有,由此可得所选3人恰有1名女生的概率.(3)方法一:用A表示所选3人均为男生,则 表示所选
表示所选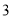 人中至少有
人中至少有 名女生,所以根据对立事件的和为1,即可求出答案; 方法二:用B表示恰有1名女生,用C表示两名女生均当选,则B+C表示所选
名女生,所以根据对立事件的和为1,即可求出答案; 方法二:用B表示恰有1名女生,用C表示两名女生均当选,则B+C表示所选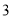 人中至少有
人中至少有 名女生,由于事件B与C互斥,且P(B)=
名女生,由于事件B与C互斥,且P(B)= 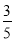 ,P(C)=
,P(C)= 
所以P(B+C)=P(B)+P(C)即可求出答案.
【解析】
从4男2女中任选3人,用无序数对(x,y,z)表示如下:其中1,2,3,4为男,5,6为女
(1,2,3),(1,2,4),(1,2,5),(1,2,6),(1,3,4),(1,3,5),(1,3,6),(1,4,5),
(1,4,6),(1,5,6),(2,3,4),(2,3,5),(2,3,6),(2,4,5),(2,4,6),(2,5,6),(3,4,5),
(3,4,6),(3,5,6),(4,5,6)共20种结果,每种出现的可能性相同,故试验属古典概型。
(1)用A表示所选3人均为男生,则事件A包含的基本事件有4个,则P(A)=  ;
;
(2)用B表示恰有1名女生,则事件B包含的基本事件有12个,则P(B)= ;
;
(3)方法一:用A表示所选3人均为男生,则 表示所选
表示所选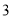 人中至少有
人中至少有 名女生,
名女生,
所以P( )=1-P(A)=1-
)=1-P(A)=1- =
= ;
;
方法二:用C表示两名女生均当选,则B+C表示所选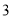 人中至少有
人中至少有 名女生,
名女生,
由于事件B与C互斥,且P(B)= 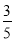 ,P(C)=
,P(C)= 
所以P(B+C)=P(B)+P(C)= 
综上可知:(1)所选3人均为男生的概率为 ;
;
(2)所选3人中恰有1名女生的概率为
(3)所选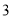 人中至少有
人中至少有 名女生的概率为
名女生的概率为
考点:古典概型及其概率计算公式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2016届陕西省高一下学期期中考试数学试卷(解析版) 题型:选择题
要得到函数 的图像,只需将函数
的图像,只需将函数 的图像 ( )
的图像 ( )
A.向左平移 个单位 B.向右平移
个单位 B.向右平移 个单位
个单位
C.向左平移 个单位 D.向右平移
个单位 D.向右平移 个单位
个单位
查看答案和解析>>
科目:高中数学 来源:2016届陕西省高一上学期期末考试数学试卷(解析版) 题型:选择题
定义在 上的函数
上的函数 满足对任意的
满足对任意的 ,有
,有 .则满足
.则满足 <
< 的x取值范围是( )
的x取值范围是( )
A.( ,
, ) B.[
) B.[ ,
, ) C. (
) C. ( ,
, ) D.[
) D.[ ,
, )
)
查看答案和解析>>
科目:高中数学 来源:2016届陕西省安康市高一上学期期末质量检测数学试卷(解析版) 题型:选择题
已知三条直线 ,三个平面
,三个平面 ,下列四个命题中,正确的是( )
,下列四个命题中,正确的是( )
A.
 ∥
∥ B.
B. C.
C. D.
D. m∥n
m∥n
查看答案和解析>>
科目:高中数学 来源:2016届陕西省高一下学期期中考试数学试卷(解析版) 题型:解答题
某商店统计了最近6个月某商品的进价x(元)与售价y(元)的对应数据如下表:
x | 3 | 5 | 2 | 7 | 8 | 11 |
y | 4 | 6 | 3 | 9 | 12 | 14 |
则回归直线方程是_______________.
注:线性回归直线方程系数公式:
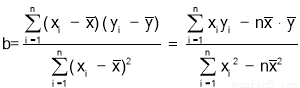 ,a=y-bx
,a=y-bx
查看答案和解析>>
科目:高中数学 来源:2016届陕西省高一下学期期中考试数学试卷(解析版) 题型:选择题
一个射手进行射击,记事件E1:“脱靶”,E2:“中靶”,E3:“中靶环数大于4”,E4:“中靶环数不小于5”,则在上述事件中,互斥而不对立的事件共有 ( ).
A.1对 B.2对 C.3对 D.4对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com