
(1)求实数a的值所组成的集合A;
(2)设关于x的方程![]() =
=![]() 的两根为x1、x2,试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及?t∈?[-1,1]恒成立?若存在,求出m的范围;若不存在,请说明理由.
的两根为x1、x2,试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及?t∈?[-1,1]恒成立?若存在,求出m的范围;若不存在,请说明理由.
解析:(1)f′(x)=![]() ,?
,?
∵![]() 在[-1,1]上是增函数,∴
在[-1,1]上是增函数,∴![]() ≥0对x∈[-1,1]恒成立,即x2-ax-2≤0.对x∈[-1,1]恒成立.?
≥0对x∈[-1,1]恒成立,即x2-ax-2≤0.对x∈[-1,1]恒成立.?
设φ(x)=x2-ax-2,![]() .?
.?
∵对x∈[-1,1],![]() 是连续函数,且当a=1时,f′(-1)=0以及当a=-1时f′(1)=0. ∴A={a|-1≤a≤1}.?
是连续函数,且当a=1时,f′(-1)=0以及当a=-1时f′(1)=0. ∴A={a|-1≤a≤1}.?
(2)由![]() =
=![]() ,得x2-ax-2=0.?
,得x2-ax-2=0.?
∵Δ=a2+8>0,∴x1、x2是方程x2-ax-2=0的两实根.?
∴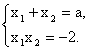
从而|x1-x2|=![]() .?
.?
∵-1≤a≤1,∴|x1-x2|=![]() ≤3.?
≤3.?
要使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立.?
当且仅当m2+tm+1≥3对任意t∈[-1,1]恒成立,即m2+tm-2≥0对任意t∈[-1,1]恒成立.?
设g(t)=m2+tm-2=mt+(m2-2),?
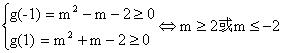 .?
.?
所以存在实数m使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,其取值范围是{m|m≥2或m≤-2}.


科目:高中数学 来源:佛山市南海一中2007届高三第三次模拟考、数学(文科)试卷 题型:044
| |||||||||||
查看答案和解析>>
科目:高中数学 来源: 题型:
(14分)已知函数![]() (x∈R)在区间[-1,1]上是增函数
(x∈R)在区间[-1,1]上是增函数
(Ⅰ)求实数a的值所组成的集合A
(Ⅱ)设关于x的方程![]() 的两实数根为x1、x2,试问:是否存在实数m,使得不等式
的两实数根为x1、x2,试问:是否存在实数m,使得不等式![]() 对任意a∈A及t∈[-1,1]恒成立?若存在,求出m的取值范围;若不存在,请说明理由?
对任意a∈A及t∈[-1,1]恒成立?若存在,求出m的取值范围;若不存在,请说明理由?
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)已知函数![]() (x∈R)在区间[-1,1]上是增函数(Ⅰ)求实数a的值所组成的集合A(Ⅱ)设关于x的方程
(x∈R)在区间[-1,1]上是增函数(Ⅰ)求实数a的值所组成的集合A(Ⅱ)设关于x的方程![]() 的两实数根为x1、x2.
的两实数根为x1、x2.
试问:
是否存在实数m,使得不等式![]() 对任意a∈A及t∈[-1,1]恒成立?若存在,求出m的取值范围;若不存在,请说明理由?
对任意a∈A及t∈[-1,1]恒成立?若存在,求出m的取值范围;若不存在,请说明理由?
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省高三第二次月考理科数学卷 题型:解答题
(本小题满分14分)已知函数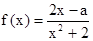 (x∈R)在区间[-1,1]上是增函数.
(x∈R)在区间[-1,1]上是增函数.
(Ⅰ)求实数a的值所组成的集合A;
(Ⅱ)设关于x的方程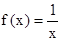 的两实数根为x1、x2,试问:是否存在实数m,使得不等式
的两实数根为x1、x2,试问:是否存在实数m,使得不等式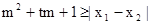 对任意a∈A及t∈[-1,1]恒成立?若存在,求出m的取值范围;若不存在,请说明理由?
对任意a∈A及t∈[-1,1]恒成立?若存在,求出m的取值范围;若不存在,请说明理由?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com