
分析 根据题意,先求出甲每局获胜的概率p,再计算打满3局、打满5局以及打满7局甲获胜的概率,求和即可.
解答 解:比赛进行到第3局结束,应满足甲连胜3局,或乙连胜3局,
则p3+(1-p)3=$\frac{1}{3}$,
化简得,9p2-9p+2=0,
解得p=$\frac{2}{3}$,p=$\frac{1}{3}$(不合题意,舍去);
所以,打满3局甲获胜的概率为${C}_{3}^{3}$•${(\frac{2}{3})}^{3}$=$\frac{8}{27}$,
打满5局甲获胜时,前3局甲2胜第4、5局甲连胜,
其概率为${C}_{3}^{2}$•${(\frac{2}{3})}^{2}$•$\frac{1}{3}$•$\frac{2}{3}$•$\frac{2}{3}$=$\frac{16}{81}$,
打满7局甲获胜时,前5局甲3胜6、7甲连胜,
其概率为${C}_{5}^{3}$•${(\frac{2}{3})}^{3}$•${(\frac{1}{3})}^{2}$•$\frac{2}{3}$•$\frac{2}{3}$=$\frac{320}{729×3}$;
所以,甲获胜的概率为P=$\frac{8}{27}$+$\frac{16}{81}$+$\frac{320}{729×3}$=$\frac{1400}{2187}$.
故答案为:$\frac{1400}{2187}$.
点评 本题考查了相互独立事件的概率计算问题,也考查了一定的计算能力,是综合性题目.


科目:高中数学 来源:2017届安徽淮北十二中高三上月考二数学(文)试卷(解析版) 题型:选择题
已知定义域为 的函数
的函数 ,若对任意的
,若对任意的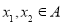 ,有
,有 ,则称函数
,则称函数 为“定义域上的
为“定义域上的 函数”,以下五个函数:①
函数”,以下五个函数:① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ ,其中是“定义上的
,其中是“定义上的 函数”的有( )
函数”的有( )
A.2个 B.3个 C.4个 D.5个
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{15}$ | B. | 4 | C. | $\sqrt{17}$ | D. | 3$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源:2017届安徽淮北十二中高三上月考二数学(理)试卷(解析版) 题型:解答题
设 为奇函数,
为奇函数, 为常数.
为常数.
(1)求 的值;
的值;
(2)判断函数 在
在 上的单调性,并说明理由;
上的单调性,并说明理由;
(3)若对于区间 上的每一个
上的每一个 值,不等式
值,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com