
为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下
| | 男 | 女 | 合计 |
| 需要 | 40 | 30 | |
| 不需要 | 160 | 270 | |
| 合计 | | | |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
(1)详见解析; (2)9.967(3)分层抽样
解析试题分析:(1)考察学生比例估值(2)考察学生对独立检验的理解与应用,先根据表格确定观测值.(3)比较分层抽样与简单抽样的优劣点.
试题解析:(1) 男 女 合计 需要 40 30 70 不需要 160 270 430 合计 200 300 500
表格填对得2分,调查的500位老年人中有70位需要志愿者提供帮助,因此该地区老年人中,需要志愿者提供帮助的老年人的比例的估计值为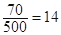 %. 4分
%. 4分
(2)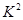 的观测值
的观测值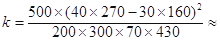 9.967. 8分
9.967. 8分
由于9.967>6.635, 9分
所以在犯错误的概率不超过0.01的前提下认为该地区的老年人是否需要帮助与性别有关系. 10分
(3)由(2)的结论知,该地区老年人是否需要帮助与性别有关,并且从样本数据能看出该地区男性老
年人与女性老年人中需要帮助的比例有明显差异,因此在调查时,先确定该地区老年人中男、女
的比例,再把老年人分成男、女两层并采用分层抽样方法比采用简单随机抽样方法更好. 12分
考点:独立性检验,分层抽样


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:解答题
打鼾不仅影响别人休息,而且可能与患某种疾病有关.下表是一次调查所得的数据,(1)将本题的2*2联表格补充完整。
(2)用提示的公式计算,每一晚都打鼾与患心脏病有关吗?
提示:
| | 患心脏病 | 未患心脏病 | 合计 |
| 每一晚都打鼾 | 3 | 17 | a = |
| 不打鼾 | 2 | 128 | b = |
| 合计 | c = | d = | n = |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某网站体育版块足球栏目组发起了“射手的连续进球与射手在场上的区域位置有关系”的调查活动,在所有参与调查的人中,持“有关系”“无关系”“不知道”态度的人数如表所示:
| | 有关系 | 无关系 | 不知道 |
| 40岁以下 | 800 | 450 | 200 |
| 40岁以上(含40岁) | 100 | 150 | 300 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题: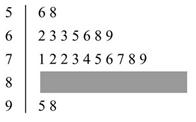
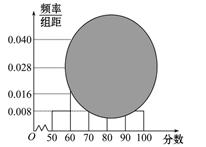
(1)求分数在[50,60)的频率及全班人数;
(2)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市交管部门为了宣传新交规举办交通知识问答活动,随机对该市15~65岁的人群抽样,回答问题统计结果如图表所示.
| 组别 | 分组 | 回答正确的人数 | 回答正确的人数占本组的概率 |
| 第1组 | [15,25) | 5 | 0.5 |
| 第2组 | [25,35) | 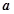 | 0.9 |
| 第3组 | [35,45) | 27 |  |
| 第4组 | [45,55) | 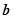 | 0.36 |
| 第5组 | [55,65) | 3 |  |
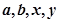 的值;
的值;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某中学一名数学老师对全班50名学生某次考试成绩分男女生进行了统计(满分150分),其中120分(含120分)以上为优秀,绘制了如下的两个频率分布直方图:
男生
女生
(1)根据以上两个直方图完成下面的2×2列联表:
| 成绩性别 | 优秀 | 不优秀 | 总计 |
| 男生 | | | |
| 女生 | | | |
| 总计 | | | |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 ,其中n=a+b+c+d.)
,其中n=a+b+c+d.)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某车间 名工人年龄数据如下表:
名工人年龄数据如下表:
| 年龄(岁) | 工人数(人) |
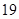 |  |
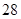 |  |
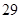 |  |
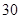 | 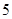 |
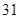 |  |
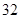 |  |
 |  |
| 合计 |  |
 名工人年龄的众数与极差;
名工人年龄的众数与极差; 名工人年龄的茎叶图;
名工人年龄的茎叶图; 名工人年龄的方差.
名工人年龄的方差.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某学校餐厅新推出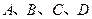 四款套餐,某一天四款套餐销售情况的条形图如下.为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
四款套餐,某一天四款套餐销售情况的条形图如下.为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
| | 满意 | 一般 | 不满意 |
| A套餐 | 50% | 25% | 25% |
| B套餐 | 80% | 0 | 20% |
| C套餐 | 50% | 50% | 0 |
| D套餐 | 40% | 20% | 40% |
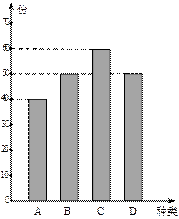
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com