
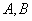 为两个事件,且
为两个事件,且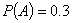 ,
,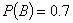 ,则( )
,则( )A.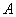 与 与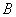 互斥 互斥 | B.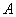 与 与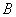 对立 对立 | C.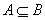 | D.A、B、C都不对 |
科目:高中数学 来源:不详 题型:解答题
| | 男 | 女 | 总计 |
| 看营养说明 | 50 | 30 | 80 |
| 不看营养说明 | 10 | 20 | 30 |
| 总计 | 60 | 50 | 110 |
 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
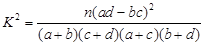 ,其中
,其中 )
)
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.5个 | B.15个 | C.10个 | D.8个 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
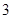 人参加当天的闯关比赛,已知甲获奖的概率为
人参加当天的闯关比赛,已知甲获奖的概率为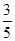 ,乙获奖的概率为
,乙获奖的概率为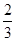 ,丙获奖而甲没有获奖的概率为
,丙获奖而甲没有获奖的概率为 。
。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
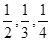 ,且每位同学能否通过考试时相互独立的。
,且每位同学能否通过考试时相互独立的。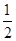 ,求这三位同学中恰好有一位同学考上大学的概率。
,求这三位同学中恰好有一位同学考上大学的概率。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A. | B.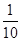 | C. | D.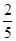 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
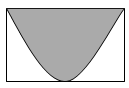
A.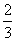 | B.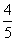 |
C.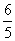 | D.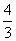 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
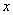 ,
,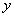 .现 从中任取3张卡片,假设每张卡片被取出的可能性相同.
.现 从中任取3张卡片,假设每张卡片被取出的可能性相同.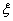 表示三张卡片上的数字之和.当三张卡片中含有字母时,则约定:有一个字母和二个相同数字时
表示三张卡片上的数字之和.当三张卡片中含有字母时,则约定:有一个字母和二个相同数字时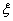 为这二个数字之和,否则
为这二个数字之和,否则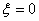 ,求
,求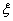 的分布列和期望
的分布列和期望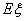 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 个红球,
个红球, 个白球(
个白球( ,且
,且 );乙的箱子里面放有2个红球,1个白球,1个黄球.现在甲从自己的箱子里任取2个球,乙从自己的箱子里任取1个球.若取出的3个球颜色都不相同,则甲获胜.
);乙的箱子里面放有2个红球,1个白球,1个黄球.现在甲从自己的箱子里任取2个球,乙从自己的箱子里任取1个球.若取出的3个球颜色都不相同,则甲获胜. 的分布列.
的分布列.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com