抛物线x2=-2y中斜率为2的平行弦(动弦)的中点的轨迹方程是 .
【答案】
分析:设出直线方程和两个交点坐标,与抛物线方程联立消去y,利用判别式大于0求得b的范围,同时根据韦达定理分别求得x
1+x
2的值,利用直线方程求得y
1+y
2的表达式,设出AB的中点的坐标,可求得x=-2,同时根据b的范围可确定y的范围,最后可求得所求的轨迹方程.
解答:解:设直线方程为y=2x+b
设两个交点为A(x
1,y
1),B(x
2,y
2)联立抛物线x
2=-2y与直线方程y=2x+b,
消去y,可得x
2+4x+2b=0△=16-4•1•2b>0∴b<2 ①
另根据韦达定理有:x
1+x
2=-4 ②
而A(x
1,y
1),B(x
2,y
2)都在直线y=2x+b上,可分别代入得到:y
1=2x
1+b y
2=2x
2+b
∴y
1+y
2=2(x
1+x
2)+2b将②代入上式,可得:y
1+y
2=2b-8 ③
设AB的中点M(x,y),可根据中点坐标公式表示为:x=
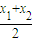
y=
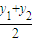
分别将②,③代入,可得:x=-2 y=b-4
由条件①:b<2,可得:y=b-4<2-4<-2
∴M点(即动弦AB中点)的轨迹方程时:x=-2这条直线位于y=-2之下的部分,
即轨迹方程x+2=0(y<-2)
故答案为:x+2=0(y<-2)
点评:本题主要考查了直线与抛物线的位置关系,求轨迹方程问题等.一般是把直线方程与抛物线方程联立,利用韦达定理求得问题的解决的途径.

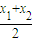
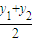 分别将②,③代入,可得:x=-2 y=b-4
分别将②,③代入,可得:x=-2 y=b-4
