
设l的方程为y=![]() x,动点M到l的距离与到x轴距离之和为3的点的轨迹是
x,动点M到l的距离与到x轴距离之和为3的点的轨迹是
矩形
圆
椭圆
双曲线
科目:高中数学 来源:广东省海丰县彭湃中学2008届高三年级入学考试数学(理) 题型:044
设抛物线过定点A(-1,0),且以直线x=1为准线.
(Ⅰ)求抛物线顶点的轨迹C的方程;
(Ⅱ)若直线l与轨迹C交于不同的两点M,N,且线段MN恰被直线![]() 平分,设弦MN的垂直平分线的方程为y=kx+m,试求m的取值范围.
平分,设弦MN的垂直平分线的方程为y=kx+m,试求m的取值范围.
查看答案和解析>>
科目:高中数学 来源:广东省海丰县彭湃中学2008届高三年级入学考试数学(文) 题型:044
设抛物线过定点A(-1,0),且以直线x=1为准线.
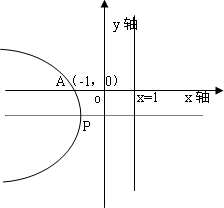
(Ⅰ)求抛物线顶点P的轨迹C的方程;
(Ⅱ)若直线l与轨迹C交于不同的两点M,N,且线段MN恰被直线![]() 平分,设弦MN的垂直平分线的方程为y=kx+m,试求m的取值范围.
平分,设弦MN的垂直平分线的方程为y=kx+m,试求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
设直线l的方程为(a+1)x+y-2-a=0(a∈R).
(1)若直线l在两坐标轴上的截距相等,求直线l的方程;
(2)若a>-1,直线l与x、y轴分别交于M、N两点,O为坐标原点,求△OMN面积取最小值时,直线l对应的方程.
查看答案和解析>>
科目:高中数学 来源:2013届山西省晋商四校高二下学期联考理科数学试卷(解析版) 题型:解答题
已知椭圆的长轴长为 ,焦点是
,焦点是 ,点
,点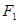 到直线
到直线 的距离为
的距离为 ,过点
,过点 且倾斜角为锐角的直线
且倾斜角为锐角的直线 与椭圆交于A、B两点,使得
与椭圆交于A、B两点,使得 .
.
(1)求椭圆的标准方程; (2)求直线l的方程.
【解析】(1)中利用点F1到直线x=- 的距离为
的距离为 可知-
可知- +
+ =
= .得到a2=4而c=
.得到a2=4而c= ,∴b2=a2-c2=1.
,∴b2=a2-c2=1.
得到椭圆的方程。(2)中,利用 ,设出点A(x1,y1)、B(x2,y2).,借助于向量公式
,设出点A(x1,y1)、B(x2,y2).,借助于向量公式 再利用 A、B在椭圆
再利用 A、B在椭圆 +y2=1上, 得到坐标的值,然后求解得到直线方程。
+y2=1上, 得到坐标的值,然后求解得到直线方程。
解:(1)∵F1到直线x=- 的距离为
的距离为 ,∴-
,∴- +
+ =
= .
.
∴a2=4而c= ,∴b2=a2-c2=1.
,∴b2=a2-c2=1.
∵椭圆的焦点在x轴上,∴所求椭圆的方程为 +y2=1.……4分
+y2=1.……4分
(2)设A(x1,y1)、B(x2,y2).由第(1)问知
 ,
,
∴ ……6分
……6分
∵A、B在椭圆 +y2=1上,
+y2=1上,
∴ ……10分
……10分
∴l的斜率为 =
= .
.
∴l的方程为y= (x-
(x- ),即
),即 x-y-
x-y- =0.
=0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com