
【题目】设函数![]() .
.
(1)若![]() 在
在![]() 处取到极值
处取到极值![]() ,求
,求![]() ,
,![]() 的值,并求
的值,并求![]() 的单调区间;
的单调区间;
(2)若对任意![]() ,都存在
,都存在![]() (
(![]() 为自然对数的底数),使得
为自然对数的底数),使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;单调增区间为
;单调增区间为![]() ,单调减区间为
,单调减区间为![]() ;(2)
;(2)![]() .
.
【解析】
(1)首先求出导函数,根据题意可得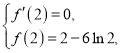 ,求出
,求出![]() ,
,![]() 的值,然后令
的值,然后令![]() ,求出单调递增区间,令
,求出单调递增区间,令![]() ,求出单调递减区间.
,求出单调递减区间.
(2)令![]() ,
,![]() ,
,![]() 是关于
是关于![]() 的一次函数且为减函数,根据题意只需令
的一次函数且为减函数,根据题意只需令![]() ,存在
,存在![]() ,使得
,使得![]() 即可,求出
即可,求出![]() ,令
,令![]() ,讨论
,讨论![]() 的取值范围,确定
的取值范围,确定![]() 的单调性,根据函数的单调性即可求解.
的单调性,根据函数的单调性即可求解.
解:(1)![]() ,
,
由题意,得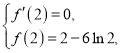 ,
,
即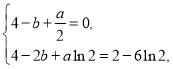 ,解得
,解得![]()
所以![]() ,
,![]() .
.
所以![]() ,
,![]() .
.
令![]() ,解得
,解得![]() .令
.令![]() ,解得
,解得![]() .
.
所以![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() .
.
(2)令![]() ,
,![]() ,
,
则![]() 是关于
是关于![]() 的一次函数且为减函数,
的一次函数且为减函数,
由题意,对任意![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立,.
成立,.
则![]() 在
在![]() 有解.
有解.
令![]() ,只需存在
,只需存在![]() ,使得
,使得![]() 即可.
即可.
由于![]() ,
,
令![]() ,
,![]() ,则
,则![]() 在
在![]() 上递增,
上递增,![]() .
.
①当![]() 时,
时,![]() ,
,![]() ,即
,即![]() ,
,![]() 在
在![]() 单调递增,
单调递增,
故![]() ,不符合题意.
,不符合题意.
②当![]() 时,
时,![]() ,
,![]() ,
,
若![]() ,则
,则![]() ,
,
所以在![]() 上
上![]() 恒成立,即
恒成立,即![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上单调递减,
上单调递减,
所以存在![]() ,使得
,使得![]() ,符合题意.
,符合题意.
若![]() ,则
,则![]() ,所以在
,所以在![]() 上一定存在实数
上一定存在实数![]() ,使得
,使得![]() ,
,
所以在![]() 上
上![]() 恒成立,即
恒成立,即![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上单调递减,
上单调递减,
所以存在![]() ,使得
,使得![]() ,符合题意.
,符合题意.
综上所述,当![]() 时,对任意
时,对任意![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立.
成立.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两位同学参加某个知识答题游戏节目,答题分两轮,第一轮为“选题答题环节”第二轮为“轮流坐庄答题环节”.首先进行第一轮“选题答题环节”,答题规则是:每位同学各自从备选的5道不同题中随机抽出3道题进行答题,答对一题加10分,答错一题(不答视为答错)减5分,已知甲能答对备选5道题中的每道题的概率都是![]() ,乙恰能答对备选5道题中的其中3道题;第一轮答题完毕后进行第二轮“轮流坐庄答题环节”,答题规则是:先确定一人坐庄答题,若答对,继续答下一题…,直到答错,则换人(换庄)答下一题…以此类推.例如若甲首先坐庄,则他答第1题,若答对继续答第2题,如果第2题也答对,继续答第3题,直到他答错则换成乙坐庄开始答下一题,…直到乙答错再换成甲坐庄答题,依次类推两人共计答完20道题游戏结束,假设由第一轮答题得分期望高的同学在第二轮环节中最先开始作答,且记第
,乙恰能答对备选5道题中的其中3道题;第一轮答题完毕后进行第二轮“轮流坐庄答题环节”,答题规则是:先确定一人坐庄答题,若答对,继续答下一题…,直到答错,则换人(换庄)答下一题…以此类推.例如若甲首先坐庄,则他答第1题,若答对继续答第2题,如果第2题也答对,继续答第3题,直到他答错则换成乙坐庄开始答下一题,…直到乙答错再换成甲坐庄答题,依次类推两人共计答完20道题游戏结束,假设由第一轮答题得分期望高的同学在第二轮环节中最先开始作答,且记第![]() 道题也由该同学(最先答题的同学)作答的概率为
道题也由该同学(最先答题的同学)作答的概率为![]() (
(![]() ),其中
),其中![]() ,已知供甲乙回答的20道题中,甲,乙两人答对其中每道题的概率都是
,已知供甲乙回答的20道题中,甲,乙两人答对其中每道题的概率都是![]() ,如果某位同学有机会答第
,如果某位同学有机会答第![]() 道题且回答正确则该同学加10分,答错(不答视为答错)则减5分,甲乙答题相互独立;两轮答题完毕总得分高者胜出.回答下列问题
道题且回答正确则该同学加10分,答错(不答视为答错)则减5分,甲乙答题相互独立;两轮答题完毕总得分高者胜出.回答下列问题
(1)请预测第二轮最先开始作答的是谁?并说明理由
(2)①求第二轮答题中![]() ,
,![]() ;
;
②求证![]() 为等比数列,并求
为等比数列,并求![]() (
(![]() )的表达式.
)的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校实行新课程改革,即除语、数、外三科为必考科目外,还要在理、化、生、史、地、政六科中选择三科作为选考科目.已知某生的高考志愿为某大学环境科学专业,按照该大学上一年高考招生选考科目要求理、化必选,为该生安排课表(上午四节、下午四节,每门课每天至少一节),已知该生某天最后两节为自习课,且数学不排下午第一节,语文、外语不相邻(上午第四节和下午第一节不算相邻),则该生该天课表有( ).
A.444种B.1776种C.1440种D.1560种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,抛物线上的点
,抛物线上的点![]() 到焦点的距离为2.
到焦点的距离为2.
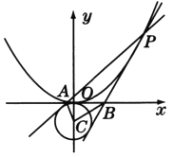
(1)求抛物线的方程和![]() 的值;
的值;
(2)如图,![]() 是抛物线上的一点,过
是抛物线上的一点,过![]() 作圆
作圆![]() 的两条切线交
的两条切线交![]() 轴于
轴于![]() ,
,![]() 两点,若
两点,若![]() 的面积为
的面积为![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过![]() 轴正半轴上的动点
轴正半轴上的动点![]() 作曲线
作曲线![]() :
:![]() 的切线,切点为
的切线,切点为![]() ,
,![]() ,线段
,线段![]() 的中点为
的中点为![]() ,设曲线
,设曲线![]() 与
与![]() 轴的交点为
轴的交点为![]() .
.
(1)求![]() 的大小及
的大小及![]() 的轨迹方程;
的轨迹方程;
(2)当动点![]() 到直线
到直线![]() 的距离最小时,求
的距离最小时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为确定数学成绩与玩手机之间的关系,从全校随机抽样调查了40名同学,其中40%的人玩手机.这40位同学的数学分数(百分制)的茎叶图如图所示.
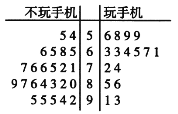
数学成绩不低于70分为良好,低于70分为一般.
(1)根据以上资料完成下面的![]() 列联表,并判断有多大把握认为“数学成绩良好与不玩手机有关系”.
列联表,并判断有多大把握认为“数学成绩良好与不玩手机有关系”.
良好 | 一般 | 总计 | |
不玩手机 | |||
玩手机 | |||
总计 | 40 |
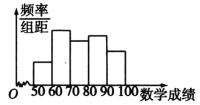
(2)现将40名同学的数学成绩分为如下5组:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .其频率分布直方图如图所示.计算这40名同学数学成绩的平均数,由茎叶图得到的真实值记为
.其频率分布直方图如图所示.计算这40名同学数学成绩的平均数,由茎叶图得到的真实值记为![]() ,由频率分布直方图得到的估计值记为
,由频率分布直方图得到的估计值记为![]() (同一组中的数据用该组区间的中点值作代表),求
(同一组中的数据用该组区间的中点值作代表),求![]() 与
与![]() 的误差值.
的误差值.
(3)从这40名同学数学成绩高于90分的7人中随机选取2人介绍学习方法,求这2保不玩手机的人数![]() 的分布列和数学期望.
的分布列和数学期望.
附: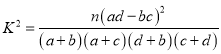 ,这40名同学的数学成绩总和为2998分.
,这40名同学的数学成绩总和为2998分.
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】央视传媒为了解央视举办的“朗读者”节目的收视时间情况,随机抽取了某市名![]() 观众进行调查,其中有
观众进行调查,其中有![]() 名男观众和
名男观众和![]() 名女观众,将这
名女观众,将这![]() 名观众收视时间编成如图所示的茎叶图(单位:分钟),收视时间在
名观众收视时间编成如图所示的茎叶图(单位:分钟),收视时间在![]() 分钟以上(包括
分钟以上(包括![]() 分钟)的称为“朗读爱好者”,收视时间在
分钟)的称为“朗读爱好者”,收视时间在![]() 分钟以下(不包括
分钟以下(不包括![]() 分钟)的称为“非朗读爱好者”.
分钟)的称为“非朗读爱好者”.

(1)若采用分层抽样的方法从“朗读爱好者”和“非朗读爱好者”中随机抽取![]() 名,再从这
名,再从这![]() 名观众中任选
名观众中任选![]() 名,求至少选到
名,求至少选到![]() 名“朗读爱好者”的概率;
名“朗读爱好者”的概率;
(2)若从收视时间在40分钟以上(包括40分钟)的所有观众中选出男、女观众各1名,求选出的这两名观众时间相差5分钟以上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某互联网公司为了确定下一季度的前期广告投入计划,收集了近![]() 个月广告投入量
个月广告投入量![]() (单位:万元)和收益
(单位:万元)和收益![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
月份 |
|
|
|
|
|
|
广告投入量 |
|
|
|
|
|
|
收益 |
|
|
|
|
|
|
他们分别用两种模型①![]() ,②
,②![]() 分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
|
|
|
|
|
|
|
|

(Ⅰ)根据残差图,比较模型①,②的拟合效果,应选择哪个模型?并说明理由;
(Ⅱ)残差绝对值大于![]() 的数据被认为是异常数据,需要剔除:
的数据被认为是异常数据,需要剔除:
(ⅰ)剔除异常数据后求出(Ⅰ)中所选模型的回归方程
(ⅱ)若广告投入量![]() 时,该模型收益的预报值是多少?
时,该模型收益的预报值是多少?
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
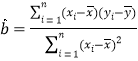
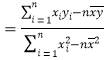 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com