(1)解:∵f(x)=

,∴f′(x)=

,x∈(0,π).
设g(x)=xcos x-sin x,x∈(0,π),则g′(x)=-xsin x<0(∵x∈(0,π)).
∴g(x)在(0,π)上为减函数,又∵g(0)=0,
∴x∈(0,π)时,g(x)<0,
∴f′(x)=

<0,
∴f(x)在(0,π)上是减函数.(6分)
(2)①解:∵(

+

)
2=1+2

,
∴x=3或4时,(

+

)
2min=1,
∴(

+

)
min=1.
又0≤a≤

+

对一切x∈[3,4]恒成立,
∴0≤a≤1.
②证明:显然当a=0,1或x=0,π时,不等式成立.
当0<a<1且0<x<π,原不等式等价于(1-a)sin(1-a)x≥(1-2a)sin x.(10分)
下面证明一个更强的不等式:(1-a)sin(1-a)x≥(1-2a+a
2)sin x=(1-a)
2sin x ①
即sin(1-a)x≥(1-a)sin x. ②
亦即

≥

.
由(1)知

在(0,π)上是减函数,又∵(1-a)x<x,∴

>

.(12分)
∴不等式②成立,从而①成立.
又∵(1-2a+a
2)sin x>(1-2a)sin x,∴(1-a)sin(1-a)x>(1-2a)sin x.
综上,∴0≤x≤π且0≤a≤1时,原不等式成立.(14分)
分析:(1)求导函数f′(x)=

,x∈(0,π),设g(x)=xcos x-sin x,x∈(0,π),求导数,可得g(x)在(0,π)上为减函数,从而x∈(0,π)时,g(x)<0,进而可得f(x)在(0,π)上是减函数;
(2)①先求得(

+

)
min=1,根据0≤a≤

+

对一切x∈[3,4]恒成立,即可求实数a的取值范围;
②显然当a=0,1或x=0,π时,不等式成立.当0<a<1且0<x<π,原不等式等价于(1-a)sin(1-a)x≥(1-2a)sin x.先证明一个更强的不等式:(1-a)sin(1-a)x≥(1-2a+a
2)sin x=(1-a)
2sin x,再根据(1-2a+a
2)sin x>(1-2a)sin x,即可得到结论.
点评:本题考查导数知识的而运用,考查函数的单调性,考查不等式的证明,有一定的综合性.

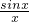
 +
+ 对一切x∈[3,4]恒成立.
对一切x∈[3,4]恒成立. ,∴f′(x)=
,∴f′(x)= ,x∈(0,π).
,x∈(0,π). <0,
<0, +
+ )2=1+2
)2=1+2 ,
, +
+ )2min=1,
)2min=1, +
+ )min=1.
)min=1. +
+ 对一切x∈[3,4]恒成立,
对一切x∈[3,4]恒成立, ≥
≥ .
. 在(0,π)上是减函数,又∵(1-a)x<x,∴
在(0,π)上是减函数,又∵(1-a)x<x,∴ >
> .(12分)
.(12分) ,x∈(0,π),设g(x)=xcos x-sin x,x∈(0,π),求导数,可得g(x)在(0,π)上为减函数,从而x∈(0,π)时,g(x)<0,进而可得f(x)在(0,π)上是减函数;
,x∈(0,π),设g(x)=xcos x-sin x,x∈(0,π),求导数,可得g(x)在(0,π)上为减函数,从而x∈(0,π)时,g(x)<0,进而可得f(x)在(0,π)上是减函数; +
+ )min=1,根据0≤a≤
)min=1,根据0≤a≤ +
+ 对一切x∈[3,4]恒成立,即可求实数a的取值范围;
对一切x∈[3,4]恒成立,即可求实数a的取值范围;

 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案