
分析 (Ⅰ)由正弦定理得$\frac{\sqrt{3}a}{cosA}=\frac{a}{sinA}$,从而tanA=$\frac{\sqrt{3}}{3}$,由此能求出A的值.
(Ⅱ)推导出B=$\frac{π}{6}$,∠C=$\frac{2π}{3}$,设AC=BC=2a,则S△ABC=$\sqrt{3}$a2=4$\sqrt{3}$,得a=2,由此利用余弦定理能求出AM.
解答 解:(Ⅰ)由正弦定理:$\frac{a}{sinA}=\frac{b}{sinB}$,又由已知$\frac{\sqrt{3}a}{cosA}=\frac{b}{sinB}$,
所以$\frac{\sqrt{3}a}{cosA}=\frac{a}{sinA}$,tanA=$\frac{\sqrt{3}}{3}$,
因为A∈(0,π),所以A=$\frac{π}{6}$.
(Ⅱ)由已知B=$\frac{π}{6}$,则△ABC是等腰三角形,∠C=$\frac{2π}{3}$,设AC=BC=2a,
S△ABC=$\frac{1}{2}AC•BC•sin∠ACB$=$\frac{1}{2}•(2a)^{2}sin\frac{2π}{3}$=$\sqrt{3}$a2,
由已知△ABC的面积为4$\sqrt{3}$,得a2=4,a=2,
△ACM中,由余弦定理,AM2=CA2+CM2-2CA•CM•cos$\frac{2π}{3}$
=42+22-2×2×4×(-$\frac{1}{2}$)=28,
所以AM=2$\sqrt{7}$.
点评 本题考查余弦定理、正弦定理、解三角形等基础知识,考查抽象概括能力、数据处理能力、运算求解能力,考查应用意识、创新意识,考查化归与转化思想、分类与整合思想,是中档题.


科目:高中数学 来源: 题型:解答题
| 年份 | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 |
| 汽车越野赛届编号x | 1 | 2 | 3 | 4 | 5 |
| 外地游客人数y(单位:十万) | 0.6 | 0.8 | 0.9 | 1.2 | 1.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | [-2,2] | C. | {-1,0,1} | D. | {-2,-1,0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $x=\frac{π}{12}$ | B. | $x=-\frac{π}{3}$ | C. | $x=-\frac{π}{6}$ | D. | $x=\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
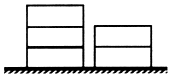 如图所示,某货场有两堆集装箱,一堆2个,一堆3个,现需要全部装运,每次只能从其中一堆取最上面的一个集装箱,则在装运的过程中不同取法的种数是( )
如图所示,某货场有两堆集装箱,一堆2个,一堆3个,现需要全部装运,每次只能从其中一堆取最上面的一个集装箱,则在装运的过程中不同取法的种数是( )| A. | 6 | B. | 10 | C. | 12 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x<4} | B. | {x|-1<x<7} | C. | {x|0<x≤4} | D. | {x|0≤x<4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com