
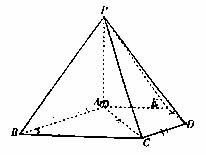
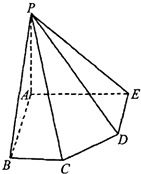
 如图,在五棱锥P—ABCDE中,
如图,在五棱锥P—ABCDE中,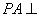 平面ABCDE,AB//CD,AC//ED,AE//BC,
平面ABCDE,AB//CD,AC//ED,AE//BC,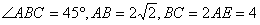 ,三角形PAB是等腰三角形。
,三角形PAB是等腰三角形。
(Ⅰ)求证:平面PCD 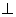 平面PAC;
平面PAC;
(Ⅱ)求直线PB与平面PCD所成角的大小;
(Ⅲ)求四棱锥P—ACDE的体积。
【解析】(Ⅰ)证明:因为 ABC=45°,
ABC=45°,
AB=2 ,BC=4,
,BC=4,
所以在 中,由余弦定理得:
中,由余弦定理得:
 ,解得
,解得 ,
,
所以 ,即
,即 ,又PA⊥平面ABCDE,所以PA⊥
,又PA⊥平面ABCDE,所以PA⊥ ,
,
又PA ,所以
,所以 ,又AB∥CD,所以
,又AB∥CD,所以 ,又因为
,又因为
 ,所以平面PCD⊥平面PAC;
,所以平面PCD⊥平面PAC;
(Ⅱ)由(Ⅰ)知平面PCD⊥平面PAC,所以在平面PAC内,
过点A作 于H,则
于H,则
 ,又AB∥CD,AB
,又AB∥CD,AB 平面
平面 内,所以AB平行于平面
内,所以AB平行于平面 ,所以点A到平面
,所以点A到平面 的距离等于点B到平面
的距离等于点B到平面 的距离,过点B作BO⊥平面
的距离,过点B作BO⊥平面 于点O,则
于点O,则 为所求角,且
为所求角,且 ,又容易求得
,又容易求得 ,
,
所以 ,即
,即 =
= ,所以直线PB与平面PCD所成角的大小为
,所以直线PB与平面PCD所成角的大小为 ;
;
(Ⅲ)由(Ⅰ)知 ,所以
,所以 ,又AC∥ED,所以四边形ACDE是直角梯形,又容易求得
,又AC∥ED,所以四边形ACDE是直角梯形,又容易求得 ,AC=
,AC= ,
,
所以四边形ACDE的面积为 ,
,
所以四棱锥P—ACDE的体积为 =
= 。
。
【命题意图】本题考查了空间几何体的线面与面面垂直、线面角的求解以及几何体的体积计算问题,考查了同学们的空间想象能力以及空间思维能力。


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
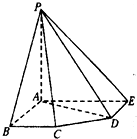 如图,在五棱锥P-ABCDE中,PA=AB=AE=2a,PB=PE=2
如图,在五棱锥P-ABCDE中,PA=AB=AE=2a,PB=PE=2| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2010-2011学年重庆市西南师大附中高三(下)第六次月考数学试卷(文科)(解析版) 题型:解答题
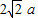 ,BC=DE=a,∠EAB=∠ABC=∠DEA=90°.
,BC=DE=a,∠EAB=∠ABC=∠DEA=90°.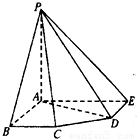
查看答案和解析>>
科目:高中数学 来源:2011年湖南省长沙市高考数学模拟试卷(理科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com