
数据 | 1 | 2 | 3 | … | n |
变量x | x1 | x2 | x3 | … | xn |
变量y | y1 | y2 | y3 | … | yn |
将以上数据,以x为自变量,y为因变量,得回归方程为![]() =bx+a;将y为自变量,x为因变量,得回归方程为
=bx+a;将y为自变量,x为因变量,得回归方程为![]() =b′y+a′.
=b′y+a′.
定义两个变量的相关关系数r的计算公式为r= ,它可表示两个变量线性关系的强弱.
,它可表示两个变量线性关系的强弱.
试问r能否用上述两方程中的b,a与b′,a′表示?如能,怎样表示?
思路解析:本题容易产生两个错解:
错解一:因为两组变量一旦确定后,两组变量间的相关关系也随之确定了,故r不是随b,a,b′,a′的变化而变化的,于是r不能用b,a及b′,a′表示.
错解二:因为b为回归方程的斜率,a为截距,斜率与截距的取值范围均为R,而相关系数r的取值范围为[-1,1],它们的取值范围不一样,因而r不能用b,a及b′,a′表示.
产生这种错解的原因是:当变量确定后,r是随之而确定了,但b,a及b′, a′也?随之而定了,上述错解一中视以上四个系数在变化,因而误认为r与它们无关而发生了错误.对于错解二,虽然对b与a及r的范围的说法均是正确的,但未曾注意到两个方程之间的相关关系,即系数b,a与b′,a′并不是两组完全独立的变量,因而也造成了解答的错误.
解:在方程![]() =bx+a中b=
=bx+a中b=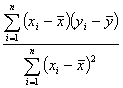 ,在方程
,在方程![]() =b′y+a′中b′=
=b′y+a′中b′= ,
,
于是bb′= .
. =
= =r2.
=r2.
故r=![]() ,
,
即r能用b,b′表示,且r=![]() .
.


科目:高中数学 来源: 题型:
两个具有线性相关关系的变量的一组数据为:
| 数据 | 1 | 2 | 3 | … | n |
| 变量x | x1 | x2 | x3 | … | xn |
| 变量y | y1 | y2 | y3 | … | yn |
将以上数据,以x为自变量,y为因变量,得回归方程为![]() =bx+a;将y为自变量,x为因变量,得回归方程为
=bx+a;将y为自变量,x为因变量,得回归方程为![]() =b′y+a′.
=b′y+a′.
定义两个变量的相关关系数r的计算公式为r= ,它可表示两个变量线性关系的强弱.
,它可表示两个变量线性关系的强弱.
试问r能否用上述两方程中的b,a与b′,a′表示?如能,怎样表示?
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖北省武汉市武昌区高二(下)期末数学试卷(理科)(解析版) 题型:填空题
 ,x∈{1,5,7,13,14},则
,x∈{1,5,7,13,14},则 = .
= .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com