
| a |
| 3 |
| b |
| 3 |
| a |
| b |
| 3 |
| 4 |
| 3 |
| 4 |
| a |
| 3 |
| b |
| 3 |
| a |
| b |
| a |
| b |
| 3 |
| 3 |
| 3 |
| 4 |
| y2 |
| 4 |
| x2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
|
-3k+6
| ||
| 3k2+4 |
-3k-6
| ||
| 3k2+4 |
| 1 |
| 2 |
12
| ||
| 3k2+4 |
| k2+1 |
12
| ||
| 3k2+4 |
| 12t |
| 3t2+1 |
| 12 | ||
3t+
|
| 1 |
| t |
| 1 |
| t2 |
| 12 |
| 4 |
| 12 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 9 |
| 16 |
| 9 |
| 16 |


科目:高中数学 来源: 题型:
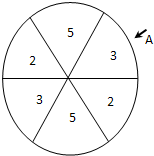 (2013•天河区三模)如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用力旋转转盘,转盘停止转动时,箭头A所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘,得分情况记为(a,b)(假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).
(2013•天河区三模)如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用力旋转转盘,转盘停止转动时,箭头A所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘,得分情况记为(a,b)(假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| b+2 | x+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com