
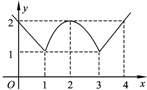
 如图,函数的图象由两条射线及抛物线的一部分组成,求函数的解析式.
如图,函数的图象由两条射线及抛物线的一部分组成,求函数的解析式.
|
|
|


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:
| ||
| 2 |

| k |
| 2 |
| k |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
下图表示了一个由区间(0,1)到实数集R的映射过程:区间(0,1)中的实数m对应数轴上的点M,如图1;将线段AB围成一个圆,使两端点A.B恰好重合,如图2;再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1),如图3。对于图3中直线AM与x轴交于点N(n ,0),则 m的象就是n,记作![]() ,
,
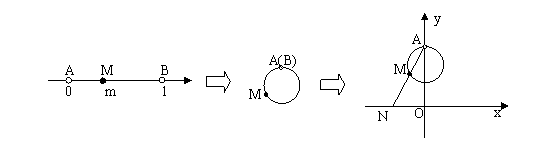
图1 图2 图3
下列说法中正确的是_______________.(填出所有正确命题的序号)
①![]() ;②
;②![]() 是奇函数;③
是奇函数;③![]() 在定义域上单调递增;
在定义域上单调递增;
④![]() 的图象关于点
的图象关于点![]() 对称;⑤
对称;⑤![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
⑥![]() 的最小正周期为1;⑦
的最小正周期为1;⑦![]() 的最大值为1。
的最大值为1。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com