
(2007
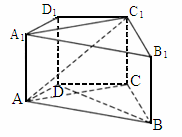
北京崇文模拟)如下图,直四棱柱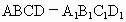 中,∠ADC=90°,△ABC为等边三角形,且
中,∠ADC=90°,△ABC为等边三角形,且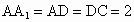 .
.
(1)
求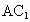 与BC所成角的余弦值;
与BC所成角的余弦值;
(2)
求二面角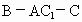 的大小;
的大小;
(3)
设M是线段BD上的点,当DM为何值时,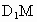 ⊥平面
⊥平面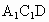 ?并证明你的结论.
?并证明你的结论.
|
解析: (1)∵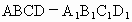 是直四棱柱, 是直四棱柱,
∴ 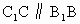 ,且 ,且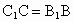 , ,
∴四边形 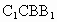 是平行四边形, 是平行四边形,
∴ 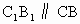 ; ;
∴即 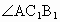 (或其补角)是 (或其补角)是 与BC所成的角. 与BC所成的角.
连接 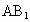 ,在三角形 ,在三角形 中, 中,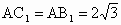 , ,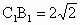 , ,
∴ 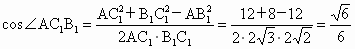 . .
故  与BC所成的角的余弦值为 与BC所成的角的余弦值为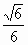 . .
(2) 设AC∩BD=O,则BO⊥AC,又  , ,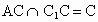 , ,
∴ BO⊥平面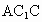 . .
过 O作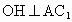 交于 交于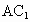 于H,连接BH,则 于H,连接BH,则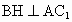 , ,
∴∠ OHB为二面角 的平面角. 的平面角.
在 Rt△BOH中,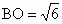 , ,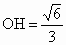 , ,
∴ 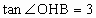 , ,
故二面角  的大小为arctan3. 的大小为arctan3.
(3) 在BD上取点M,使得OM=OD,连接 AM,CM,∵ AD=DC,∠ADC=90°,又 DO⊥AC,且AO=OC,∴ CM=AM=AD,∴四边形 ABCD是一个正方形可证 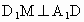 , ,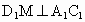 ,又 ,又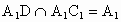 , ,
∴ 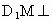 平面 平面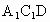 ,此时 ,此时 . .
故当 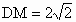 时,有 时,有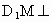 平面 平面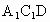 . . |


科目:高中数学 来源: 题型:044
(2007
北京崇文模拟)已知函数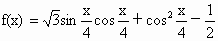 .
.
(1)
求f(x)的单调递增区间;(2)
在△ABC中,角A、B、C的对边分别是a、b、c,满足(2a-c)cos B=b cos C,求函数f(A)的取值范围.查看答案和解析>>
科目:高中数学 来源: 题型:013
(2007
北京崇文模拟)在数列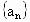 中,对任意
中,对任意 ,都有
,都有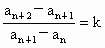 (k为常数),则称
(k为常数),则称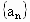 为“等差比数列”,下面对“等差比数列”的判断:①k不可能为0;②等差数列一定是等差比数列;③等比数列一定是等差比数列;④通项公式为
为“等差比数列”,下面对“等差比数列”的判断:①k不可能为0;②等差数列一定是等差比数列;③等比数列一定是等差比数列;④通项公式为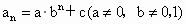 的数列一定是等差比数列,其中正确的判断
的数列一定是等差比数列,其中正确的判断
[
]|
A .①② |
B .②③ |
C .③④ |
D .①④ |
查看答案和解析>>
科目:高中数学 来源: 题型:022
(2007
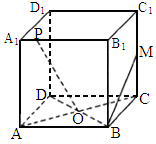
北京崇文模拟)如下图,在正方体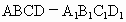 中,M是
中,M是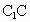 的中点,O是底面ABCD的中心,P是
的中点,O是底面ABCD的中心,P是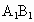 上的任意点,则直线BM与OP所成的角为__________°.
上的任意点,则直线BM与OP所成的角为__________°.
查看答案和解析>>
科目:高中数学 来源: 题型:044
(2007
北京崇文模拟)甲、乙两人各射击一次,击中目标的概率分别是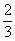 和
和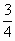 ,假设两人每次射击是否击中目标相互之间没有影响.
,假设两人每次射击是否击中目标相互之间没有影响.
(1)
求甲射击5次,有两次未击中目标的概率;(2)
假设某人连续2次未击中目标,则中止其射击,求乙恰好射击5次后,被中止射击的概率.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com