
【题目】已知数列![]() 满足:
满足:![]() ,
,![]() .
.
(1)求最小的正实数![]() ,使得对任意的
,使得对任意的![]() ,恒有
,恒有![]() ;
;
(2)求证:对任意的正整数![]() ,恒有
,恒有![]() .
.
【答案】(1)1;(2)证明见解析.
【解析】
试题分析:(1)已知条件是数列的递推式,比较复杂,在证明时,可先计算数列的前几项,如![]() .想象即归纳出结论数列
.想象即归纳出结论数列![]() 是递减数列,从而
是递减数列,从而![]() 的最小值为1,因此只要证明
的最小值为1,因此只要证明![]() ,可用数学归纳法证(2)
,可用数学归纳法证(2)
证明;(2)由(1)可得数列![]() 是单调递减的正项数列.,这样右边的证明较方便,只要重新放缩可得,
是单调递减的正项数列.,这样右边的证明较方便,只要重新放缩可得,
![]() ,从而
,从而![]() ,左边不等式的证明较难,左边先放缩为
,左边不等式的证明较难,左边先放缩为![]() ,从而
,从而![]() ,左右同除
,左右同除![]() 得:
得:![]() ,即
,即![]() ,利用累加法求
,利用累加法求![]() (其中求和
(其中求和![]() ,可用裂项相消或错位相减法求得),可证明不等式.
,可用裂项相消或错位相减法求得),可证明不等式.
试题解析:(1)由于![]() ,
,![]() ,
,![]() ,
,
由此我们可以猜想![]() 为单调递减数列,因此我们猜测
为单调递减数列,因此我们猜测![]() 的最小值为1,下面我们证明
的最小值为1,下面我们证明![]() .
.
![]() ,故当
,故当![]() 时,数列
时,数列![]() 为单调递减数列,从而
为单调递减数列,从而![]() .
.
![]() ,由于
,由于![]() ,且当
,且当![]() 时,有
时,有![]()
从而对任意的![]() ,恒有
,恒有![]() ,又由于
,又由于![]() ,从而所求的最小正实数
,从而所求的最小正实数![]() .
.
(说明:若用数学归纳法证明,也同样给满分)
事实上,由于![]() ,假设
,假设![]() 时,
时,![]() ,则当
,则当![]() 时,
时,
考虑到![]() ,从而
,从而![]() ,
,![]() .
.
从而![]() ,
,
从而由数学归纳法原理得:对任意的![]() ,恒有
,恒有![]() .
.
又由于![]() ,从而所求的最小正实数
,从而所求的最小正实数![]() .
.
(2)由于![]() ,则
,则![]() ,
,
从而数列![]() 是单调递减的正项数列.
是单调递减的正项数列.
一方面,![]() ,从而
,从而![]()
另一方面,![]() ,从而
,从而![]() ,
,
左右同除![]() 得:
得:![]() ,即
,即![]()
设
![]() (也可利用错位相减法求解
(也可利用错位相减法求解 ,两式相减得
,两式相减得
![]() ,从而
,从而
![]() )
)
从而由![]() ,得,
,得,
当![]() 时,
时,![]()
从而![]() ,即
,即 ,
,
即当![]() 时,
时,![]() ,又当
,又当![]() 时,
时,![]() ,从而对任意的
,从而对任意的![]() ,恒有
,恒有![]() .
.
综上所示,对任意的正整数![]() ,恒有
,恒有![]() .
.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,圆![]() 的方程为
的方程为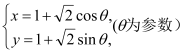 .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位长度,直线
轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位长度,直线![]() 的极坐标方程
的极坐标方程![]() .
.
(Ⅰ)当![]() 时,判断直线
时,判断直线![]() 与
与![]() 的关系;
的关系;
(Ⅱ)当![]() 上有且只有一点到直线
上有且只有一点到直线![]() 的距离等于
的距离等于![]() 时,求
时,求![]() 上到直线
上到直线![]() 距离为
距离为![]() 的点的坐标.
的点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大衍数列,来源于《乾坤谱》中对易传“大衍之数五十”的推论.主要用于解释中国传统文化中的太极衍生原理.数列中的每一项,都代表太极衍生过程中,曾经经历过的两仪数量总和,是中华传统文化中隐藏着的世界数学史上第一道数列题.其前10项依次是0,2,4,8,12,18,24,32,40,50,…则此数列第20项为
A. 180 B. 200 C. 128 D. 162
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,以原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),
为参数),![]() 与
与![]() 分别交于
分别交于![]() .
.
(Ⅰ)写出![]() 的平面直角坐标系方程和
的平面直角坐标系方程和![]() 的普通方程;
的普通方程;
(Ⅱ)若![]() 成等比数列,求
成等比数列,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从一箱产品中随机地抽取一件,设事件A={抽到一等品},事件B={抽到二等品},事件C={抽到三等品},且已知P(A)=0.65,P(B)=0.2,P(C)=0.1.则事件“抽到的是二等品或三等品”的概率为( )
A. 0.7 B. 0.65
C. 0.35 D. 0.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要从容量为102的总体中用系统抽样法随机抽取一个容量为9的样本,则下列叙述正确的是( )
A. 将总体分11组,每组间隔为9
B. 将总体分9组,每组间隔为11
C. 从总体中剔除3个个体后分11组,每组间隔为9
D. 从总体中剔除3个个体后分9组,每组间隔为11
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】利用斜二测画法画水平放置的平面图形的直观图,得到下列结论,其中正确的是( )
A.正三角形的直观图仍然是正三角形
B.平行四边形的直观图一定是平行四边形
C.正方形的直观图是正方形
D.圆的直观图是圆
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用样本估计总体,下列说法正确的是( )
A、样本的结果就是总体的结果
B、样本容量越大,估计就越精确
C、样本的标准差可以近似地反映总体的平均状态
D、数据的方差越大,说明数据越稳定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com