
甲、乙两名跳高运动员一次试跳2米高度成功的概率分别为0.7、0.6,且每次试跳成功与否相互之间没有影响,求:
(1)甲试跳三次,第三次才成功地概率;
(2)甲、乙两人在第一次试跳中至少有一人成功的概率;
(3)甲、乙各试跳两次,甲比乙的成功次数恰好多一次的概率.
(1)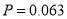 ;(2)
;(2)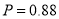 ;(3)
;(3)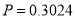
【解析】
试题分析:(1)独立重复试验是在同样的条件下重复地、各次之间相互独立地进行的一种试验,在这种试验中,每一次试验只有两种结果,即某事件要么发生,要么不发生,并且任何一次试验中发生的概率都是一样的;(2)求复杂事件的概率,要正确分析复杂事件的构成,看复杂事件能转化为几个彼此独立的事件和事件还是能转化为几个相互独立事件同时发生的积事件,然后求概率;(3)正确区分相互独立事件与互斥事件的区别
试题解析:【解析】
设“甲第i次试跳成功”为事件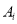 ,“乙第i次试跳成功”为事件Bi,依题意得P(
,“乙第i次试跳成功”为事件Bi,依题意得P(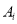 )=0.7、P(Bi)=0.6,且
)=0.7、P(Bi)=0.6,且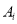 、Bi(i=1、2、3)相互独立.
、Bi(i=1、2、3)相互独立.
(1)“甲第三次试跳才成功”为事件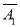
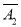 A3,且三次试跳相互独立,
A3,且三次试跳相互独立,
∴P(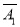
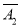 A3)=P(
A3)=P(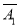 )P(
)P( )P(A3)=0.3×0.3×0.7=0.063.
)P(A3)=0.3×0.3×0.7=0.063.
即甲第三次试跳才成功的概率为0.063.
(2)“甲、乙两人在第一次试跳中至少有一人成功”为事件C,
P(C)=1-P(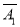 )·P(
)·P(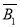 )=1-0.3×0.4=0.88.
)=1-0.3×0.4=0.88.
即甲、乙两人在第一次试跳中至少有一人成功的概率为0.88.
(3)设“甲在两次试跳中成功i次”为事件Mi(i=0、1、2),
“乙在两次试跳中成功i次”为事件Ni(i=0、1、2),
∵事件“甲、乙各试跳两次,甲比乙的成功次数恰好多一次”可表示为M1N0+M2N1,且M1N0、M2N1为互斥事件,
∴所求的概率为P(M1N0+M2N1)=P(M1N0)+P(M2N1)=P(M1)P(N0)+P(M2)P(N1)=0.7×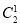 ×0.3×0.42+0.72×
×0.3×0.42+0.72×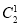 ×0.6×0.4=0.0672+0.2352=0.3024.
×0.6×0.4=0.0672+0.2352=0.3024.
即甲、乙每人试跳两次,甲比乙的成功次数恰好多一次的概率为0.3024.
考点:(1)独立事件的概率;(2)对立事件的概率.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源:2015届重庆市高二下学期期中考试文科数学试卷(解析版) 题型:解答题
(本小题满分12分,(1)小问4分,(2)小问8分)已知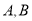 为椭圆
为椭圆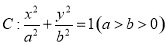 上两动点,
上两动点, 分别为其左右焦点,直线
分别为其左右焦点,直线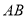 过点
过点 ,且不垂直于
,且不垂直于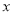 轴,
轴,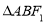 的周长为
的周长为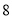 ,且椭圆的短轴长为
,且椭圆的短轴长为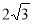 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)已知点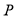 为椭圆
为椭圆 的左端点,连接
的左端点,连接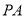 并延长交直线
并延长交直线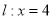 于点
于点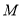 .求证:直线
.求证:直线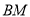 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省鞍山市高二下学期期末考试理科数学试卷(解析版) 题型:解答题
已知圆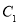 的参数方程为
的参数方程为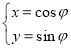 (
(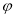 为参数),以坐标原点
为参数),以坐标原点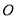 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆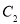 的极坐标方程为
的极坐标方程为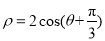 .
.
(1)将圆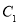 的参数方程化为普通方程,将圆
的参数方程化为普通方程,将圆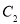 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)圆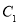 ,
,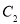 是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.
是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省鞍山市高二下学期期末考试理科数学试卷(解析版) 题型:填空题
今有2个红球、3个黄球、4个白球,同色球不加以区分,将这9个球排成一列有 种不同的方法.(用数字作答)
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省鞍山市高二下学期期末考试理科数学试卷(解析版) 题型:选择题
将三颗骰子各掷一次,设事件A为“三个点数都不相同”,事件B为“至少出现一个6点”,则概率P(A|B)的值为
A.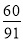 B.
B.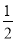 C.
C.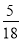 D.
D.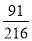
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省抚顺市六校高二下学期期末考试理科数学试卷(解析版) 题型:填空题
有甲、乙、丙三项任务,甲需2人承担,乙、丙各需1人承担,从10人中选派4人承担这项任务,不同的选法有________.
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省分校高二新疆班下学期期末数学试卷(解析版) 题型:解答题
给出四个等式:
1=1
1-4=-(1+2)
1-4+9=1+2+3
1-4+9-16=-(1+2+3+4)
……
(1)写出第5,6个等式,并猜测第n(n∈N*)个等式
(2)用数学归纳法证明你猜测的等式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com