
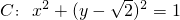 的两条切线,切点分别为A、B,若|AB|
的两条切线,切点分别为A、B,若|AB|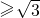 ,,则x0的取值范围是
,,则x0的取值范围是
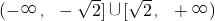
 时,M在y轴左侧,当M往右运动时,|AB|长变小,往左运动时,|AB|长变大,M在y轴右侧,刚好相反,故连接CA,CB,MC,由MA及MB为圆C的切线,根据切线性质得到CA与AM垂直,CB与BM垂直,由圆C的方程找出圆心坐标和圆的半径,可得到|AC|的长,利用HL证明三角形ACM与三角形BCM全等,再利用三线合一得到CN与AB垂直,N为AB中点,可求出|AN|的长,又直角三角形ACN与直角三角形ACM相似,根据对应边成比例可求出|CM|的长,在直角三角形COM中,利用勾股定理求出|OM|的长,可得出此时M的坐标,根据分析的规律,即可得到满足题意的x0的取值范围.
时,M在y轴左侧,当M往右运动时,|AB|长变小,往左运动时,|AB|长变大,M在y轴右侧,刚好相反,故连接CA,CB,MC,由MA及MB为圆C的切线,根据切线性质得到CA与AM垂直,CB与BM垂直,由圆C的方程找出圆心坐标和圆的半径,可得到|AC|的长,利用HL证明三角形ACM与三角形BCM全等,再利用三线合一得到CN与AB垂直,N为AB中点,可求出|AN|的长,又直角三角形ACN与直角三角形ACM相似,根据对应边成比例可求出|CM|的长,在直角三角形COM中,利用勾股定理求出|OM|的长,可得出此时M的坐标,根据分析的规律,即可得到满足题意的x0的取值范围.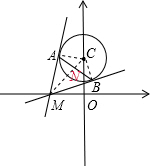
 时,由圆C的方程
时,由圆C的方程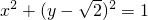 ,得到圆心C(0,
,得到圆心C(0, ),半径|CA|=|CB|=1,
),半径|CA|=|CB|=1, |AB|=
|AB|= ,
, ,
, ,|CM|=2,
,|CM|=2, ;
; ,
,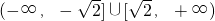 .
. 时,M在y轴左侧,当M往右运动时,|AB|长变小,往左运动时,|AB|长变大,M在y轴右侧,刚好相反是解本题的关键.
时,M在y轴左侧,当M往右运动时,|AB|长变小,往左运动时,|AB|长变大,M在y轴右侧,刚好相反是解本题的关键. 

 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
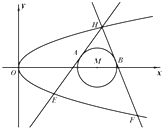 如图,已知抛物线C:y2=2px和⊙M:(x-4)2+y2=1,过抛物线C上一点H(x0,y0)作两条直线与⊙M相切于A、B两点,分别交抛物线为E、F两点,圆心点M到抛物线准线的距离为
如图,已知抛物线C:y2=2px和⊙M:(x-4)2+y2=1,过抛物线C上一点H(x0,y0)作两条直线与⊙M相切于A、B两点,分别交抛物线为E、F两点,圆心点M到抛物线准线的距离为| 17 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
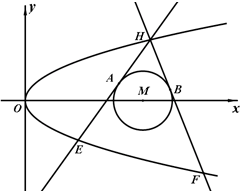 (2012•辽宁模拟)如图,已知抛物线C:y2=2px和⊙M:(x-4)2+y2=1,过抛物线C上一点H(x0,y0)(y0≥1)作两条直线与⊙M相切于A、两点,分别交抛物线为E、F两点,圆心点M到抛物线准线的距离为
(2012•辽宁模拟)如图,已知抛物线C:y2=2px和⊙M:(x-4)2+y2=1,过抛物线C上一点H(x0,y0)(y0≥1)作两条直线与⊙M相切于A、两点,分别交抛物线为E、F两点,圆心点M到抛物线准线的距离为| 17 | 4 |
查看答案和解析>>
科目:高中数学 来源:河北省正定中学2010届高三下学期第一次考试文科数学试题 题型:013
过x轴上一点M(x0,0)作圆![]() 的两条切线,切点分别为A、B.若
的两条切线,切点分别为A、B.若![]() ,则x0的取值范围是
,则x0的取值范围是
![]()
[-2,2]
![]()
(-∞,-2]∪[2,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com