Question

直线

3

x+y+1=0与圆x²+y²=1交于两点A，B，O为坐标原点，则∠AOB=

120°

．

Answer 1

分析：根据题意画出图形，如图所示，过圆心O作OD垂直于AB，根据垂径定理得到D为弦AB的中点，利用点到直线的距离公式求出圆心O到直线AB的距离d，在直角三角形OBD中，根据求出的d等于|OB|的一半，可得∠OBD为30°，又|OA|=|OB|，利用等边对等角可得∠OAD=∠OBD=30°，利用三角形内角和定理即可求出∠AOB的度数．

解答：解：根据题意画出图形，如图所示：

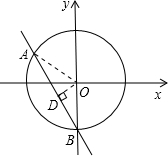
过O作OD⊥AB，根据垂径定理得D为AB的中点，
∵圆心O到直线

3

x+y+1=0的距离d=

1

( 3 )2+1

=

1

2

，
∴|OD|=

1

2

，又|OB|=r=1，且△OBD为直角三角形，
∴∠OBD=30°，又|OA|=|OB|，
∴∠OAD=∠OBD=30°，
则∠AOB=180°-2∠OBD=120°．
故答案为：120°

点评：此题考查了直线与圆的位置关系，涉及的知识有：点到直线的距离公式，垂径定理，等腰三角形及直角三角形的性质，当直线与圆相交时，常常利用弦心距、弦长的一半及圆的半径构造直角三角形，利用勾股定理及锐角三角函数来解决问题．