
 =1(a>b>0)上一点,F1、F2是椭圆的两焦点,且满足|AF1|+|AF2|=4.
=1(a>b>0)上一点,F1、F2是椭圆的两焦点,且满足|AF1|+|AF2|=4. =1
=1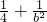 =1所以b2=
=1所以b2= ,椭圆方程为:
,椭圆方程为: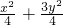 =1
=1 消去y,得(1+3k2)x2-6k(k-1)x+3k2-6k-1=0.
消去y,得(1+3k2)x2-6k(k-1)x+3k2-6k-1=0.
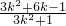
 .
.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:
| 2m |
| 3 |
| x2 |
| 4m2 |
| y2 |
| 3m2 |
| 2m |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖南省怀化市高三第二次模拟考试理科数学试卷(解析版) 题型:选择题
下图展示了一个由区间 (其中
(其中 为一正实数)到实数集R上的映射过程:区间
为一正实数)到实数集R上的映射过程:区间 中的实数
中的实数 对应线段
对应线段 上的点
上的点 ,如图1;将线段
,如图1;将线段 围成一个离心率为
围成一个离心率为 的椭圆,使两端点
的椭圆,使两端点 、
、 恰好重合于椭圆的一个短轴端点,如图2 ;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在
恰好重合于椭圆的一个短轴端点,如图2 ;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在 轴上,已知此时点
轴上,已知此时点 的坐标为
的坐标为 ,如图3,在图形变化过程中,图1中线段
,如图3,在图形变化过程中,图1中线段 的长度对应于图3中的椭圆弧ADM的长度.图3中直线
的长度对应于图3中的椭圆弧ADM的长度.图3中直线 与直线
与直线 交于点
交于点 ,则与实数
,则与实数 对应的实数就是
对应的实数就是 ,记作
,记作 ,
,

现给出下列5个命题
① ;
②函数
;
②函数 是奇函数;③函数
是奇函数;③函数 在
在 上单调递增; ④.函数
上单调递增; ④.函数 的图象关于点
的图象关于点 对称;⑤函数
对称;⑤函数 时AM过椭圆的右焦点.其中所有的真命题是: ( )
时AM过椭圆的右焦点.其中所有的真命题是: ( )
A.①③⑤ B.②③④ C.②③⑤ D.③④⑤
查看答案和解析>>
科目:高中数学 来源:2013届海南省高二上学期期末文科数学试题(解析版) 题型:解答题
(本小题满分12分)已知A,B两点是椭圆 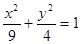 与坐标轴正半轴的两个交点.
与坐标轴正半轴的两个交点.
(1)设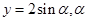 为参数,求椭圆的参数方程;
为参数,求椭圆的参数方程;
(2)在第一象限的椭圆弧上求一点P,使四边形OAPB的面积最大,并求此最大值.
查看答案和解析>>
科目:高中数学 来源:2012年四川省乐山市高考数学二模试卷(文科)(解析版) 题型:选择题
 +
+ =1左准线上一点,F1、F2分别是其左、右焦点,PF2与椭圆交于点Q,且
=1左准线上一点,F1、F2分别是其左、右焦点,PF2与椭圆交于点Q,且 =2
=2 ,则|
,则| |的值为( )
|的值为( )


查看答案和解析>>
科目:高中数学 来源:2012年四川省乐山市高考数学二模试卷(理科)(解析版) 题型:选择题
 +
+ =1左准线上一点,F1、F2分别是其左、右焦点,PF2与椭圆交于点Q,且
=1左准线上一点,F1、F2分别是其左、右焦点,PF2与椭圆交于点Q,且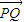 =2
=2 ,则|
,则| |的值为( )
|的值为( )


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com