
分析 将sinα+cosα=$\frac{1}{3}$两边平方,利用平方关系化简求出2sinαcosα的值,根据三角函数的符号缩小α的范围,判断出sinα-cosα的符号,利用平方关系求出sinα-cosα的值.
解答 解:将sinα+cosα=$\frac{1}{3}$两边平方得,
2sinαcosα=$-\frac{8}{9}$<0,
因为0<α<π,所以$\frac{π}{2}$<α<π,
则sinα-cosα>0,
所以sinα-cosα=$\sqrt{(sinα-cosα)^{2}}$=$\sqrt{1-(-\frac{8}{9})}$=$\frac{\sqrt{17}}{3}$.
点评 本题考查同角三角函数的平方关系,以及三角函数的符号,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
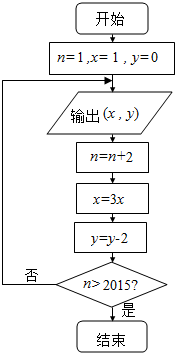 某算法的流程图如图所示,记输出的数组(x,y)依次为(x1,y1),(x2,y2),…(x3,y3)…,若程序运行中输出的一个数组是(9,y),则y=-4;程序结束时,共输出(x,y)的组数为1008.
某算法的流程图如图所示,记输出的数组(x,y)依次为(x1,y1),(x2,y2),…(x3,y3)…,若程序运行中输出的一个数组是(9,y),则y=-4;程序结束时,共输出(x,y)的组数为1008.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4(3$\sqrt{3}$+4) | B. | 8(2$\sqrt{3}$+1) | C. | 12(2$\sqrt{3}$+1) | D. | 3($\sqrt{3}$+8) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com