
定义区间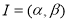 的长度为
的长度为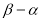 ,已知函数
,已知函数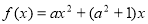 ,其中
,其中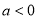 ,
,
区间 .
.
(1)求区间 的长度;
的长度;
(2)设区间 的长度函数为
的长度函数为 ,
, ,问:是否存在实数
,问:是否存在实数 ,使得
,使得
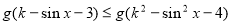 对一切
对一切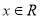 恒成立,若存在,求出
恒成立,若存在,求出 的范围;若不存在,请说明理由.
的范围;若不存在,请说明理由.
科目:高中数学 来源:2016届内蒙古赤峰市高三4月统一能力测试数学(理)试卷(解析版) 题型:选择题
已知双曲线 的两条渐近线与抛物线
的两条渐近线与抛物线 的准线分别交于
的准线分别交于 两点,
两点,  为坐标原点,若双曲线的离心率为2,则
为坐标原点,若双曲线的离心率为2,则 的面积为( )
的面积为( )
A.2 B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西高安中学高一重点班下期中数学试卷(解析版) 题型:选择题
在 中,已知
中,已知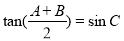 ,给出以下论断:
,给出以下论断:
① ;②
;② ;③
;③ ;④
;④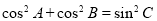 .
.
其中正确的是
A.①③ B.②④ C.①④ D.②③
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西高安中学高一重点班下期中数学试卷(解析版) 题型:选择题
已知函数 (ω>0)的最小正周期为
(ω>0)的最小正周期为 ,则该函数的图像
,则该函数的图像
A.关于直线 对称
对称
B.关于点 对称
对称
C.关于点 对称
对称
D.关于直线 对称
对称
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西高安中学高一创新班下期中数学试卷(解析版) 题型:解答题
已知 <
< <
< ,0<β<
,0<β< ,cos(
,cos( +
+ )=-
)=- ,sin(
,sin( +β)=
+β)= ,
,
求sin( +β)的值.
+β)的值.
查看答案和解析>>
科目:高中数学 来源:2016届湖南师大附中高三上学期月考六数学(理)试卷(解析版) 题型:解答题
设数列 的前
的前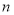 项和为
项和为 ,若存在非零常数
,若存在非零常数 ,使对任意
,使对任意 都有
都有
 成立,则称数列
成立,则称数列 为“和比数列”.
为“和比数列”.
(1)若数列 是首项为
是首项为 ,公比为
,公比为 的等比数列,判断数列
的等比数列,判断数列 是否为“和比数列”;
是否为“和比数列”;
(2)设数列 是首项为
是首项为 ,且各项互不相等的等差数列,若数列
,且各项互不相等的等差数列,若数列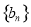 是“和比数列”,求数列
是“和比数列”,求数列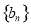 的
的
通项公式.
查看答案和解析>>
科目:高中数学 来源:2016届山西太原市高三第二次模拟考试数学(理)试卷(解析版) 题型:解答题
已知椭圆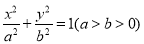 的离心率为
的离心率为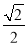 ,过焦点且垂直于长轴的弦长为
,过焦点且垂直于长轴的弦长为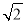 .
.
(1)已知点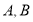 是椭圆上两点,点
是椭圆上两点,点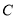 为椭圆的上顶点,
为椭圆的上顶点,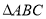 的重心恰好是椭圆的右焦点
的重心恰好是椭圆的右焦点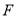 ,求
,求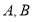 所
所
在直线的斜率;
(2)过椭圆的右焦点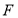 作直线
作直线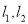 ,直线
,直线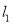 与椭圆分别交于点
与椭圆分别交于点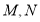 ,直线
,直线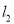 与椭圆分别交于点
与椭圆分别交于点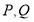 ,
,
且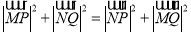 ,求四边形
,求四边形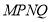 的面积
的面积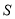 最小时直线
最小时直线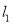 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com