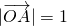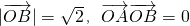练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知数学公式，数学公式，点C在∠AOB内，∠AOC=45°，设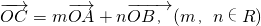数学公式，则数学公式=________．


    分析：将向量 沿 与 方向利用平行四边形原则进行分解，建立平面直角坐标系，便于计算．
    解答：如图所示，建立直角坐标系．
    则 =（1，0），=（0，），
    ∴=m +n
    =（m，n），
    ∴tan45°==1
    ∴=．
    故选B
    点评：对一个向量根据平面向量基本定理进行分解，关键是要根据平行四边形法则，找出向量在基底两个向量方向上的分量．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知椭圆的中心在坐标原点，且经过点M(1，
    2
    		5
    5
    )    ，N(-2，
    		5
    5
    )    ，若圆C的圆心与椭圆的右焦点重合，圆的半径恰好等于椭圆的短半轴长，已知点A（x，y）为圆C上的一点．
    （1）求椭圆的标准方程和圆的标准方程；
    （2）求
    AC
    •
    AO
    +2|
    AC
    -
    AO
    |    （O为坐标原点）的取值范围；
    （3）求x2+y2的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

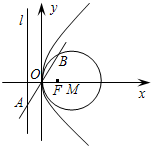    精英家教网已知抛物线C：y2=2px（p＞0）的准线为l，焦点为F．⊙M的圆心在x轴的正半轴上，且与y轴相切．过原点O作倾斜角为
    π
    3
    的直线n，交l于点A，交⊙M于另一点B，且AO=OB=2．
    （Ⅰ）求⊙M和抛物线C的方程；
    （Ⅱ）若P为抛物线C上的动点，求
    PM
    •
    PF
    的最小值；
    （Ⅲ）过l上的动点Q向⊙M作切线，切点为S，T，求证：直线ST恒过一个定点，并求该定点的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

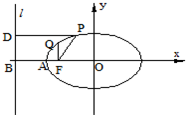    如图，已知椭圆中心在原点，F是焦点，A为顶点，准线l（椭圆上的点到焦点的距离与到准线的距离之比等于离心率）交x轴于点B，点P，Q在椭圆上，且PD⊥l于D，QF⊥AO，则①
    |PF|
    |PD|
    ；②
    |QF|
    |BF|
    ；③
    |FO|
    |AO|
    ；④
    |AF|
    |AB|
    ，其中比值为椭圆的离心率的有（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

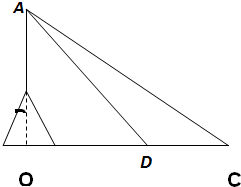    如图，某海域内的岛屿上有一直立信号塔AB，设AB延长线与海平面交于点O．测量船在点O的正东方向点C处，测得塔顶A的仰角为30°，然后测量船沿CO方向航行至D处，当CD=100（
    		3
    -1）米时，测得塔顶A的仰角为45°．
    （1）求信号塔顶A到海平面的距离AO；
    （2）已知AB=52米，测量船在沿CO方向航行的过程中，设DO=x，则当x为何值时，使得在点D处观测信号塔AB的视角∠ADB最大．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•揭阳二模）如图已知抛物线C：y2=2px（p＞0）的准线为l，焦点为F，圆M的圆心在x轴的正半轴上，且与y轴相切．过原点作倾斜角为
    π3
    的直线t，交l于点A，交圆M于点B，且|AO|=|OB|=2．
    （1）求圆M和抛物线C的方程；
    （2）试探究抛物线C上是否存在两点P，Q关于直线m：y=k（x-1）（k≠0）对称？若存在，求出直线m的方程，若不存在，说明理由．

    查看答案和解析>>

    同步练习册答案