Question

如图，已知三棱柱ABC-A₁B₁C₁的侧棱与底面所成的角为60°，AB=BC，A₁A=A₁C=2，AB⊥BC，侧面AA₁C₁C⊥底面ABC．
（1）证明：A₁B⊥A₁C₁；
（2）求二面角A-CC₁-B的大小；
（3）求经过A₁、A、B、C四点的球的表面积．

Answer 1

分析：此题可利用空间向量做：由于A₁O⊥AC，BO⊥AC，A₁A=A₁C=2故取AC中点为O则A₁O⊥AC，BO⊥AC而侧面AA₁C₁C⊥底面ABC且故可利用面面垂直的性质定理可得A₁O⊥OB所以可以OB，OC，OA₁所在的直线为x，y，z轴建立空间直角坐标系．
（1）要证明A₁B⊥A₁C₁即证明

A1B

⊥

A1C1

即说明

A1B

•

A1C1

=0即可故需求出

A1B

，

A1C1

的坐标然后利用平面向量数量积的坐标计算求出

A1B

•

A1C1

即可．
（2）分别求出面BCC₁，面ACC₁的法向量m，n然后利用向量的夹角公式cos＜

m

，

n

＞=

m • n

| m || n |

求出＜

m

，

n

＞而点B在平面ACC₁内的射影O在二面角的面ACC₁内故二面角A-CC₁-B为锐角所以二面角A-CC₁-B的大小为＜

m

，

n

＞（cos＜

m

，

n

＞＞0）或π-＜

m

，

n

＞（cos＜

m

，

n

＞＜0）．
（3）由于A₁A=A₁C，AB⊥BC，O为AC的中点故A，B，C三点所在的平面截经过A₁、A、B、C四点的球所得的截面为球的小圆而A₁O⊥平面ABC故经过A₁、A、B、C四点的球的球心在A₁O上而三角形A₁AC为正三角形故根据对称性可知球心在正三角形A₁AC的中心然后利用正三角形的性质求出球的半径再结合球的表面经公式即可得解．

解答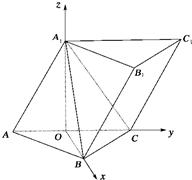：解：取AC中点为O，由A₁A=A₁C，AB=BC，知A₁O⊥AC，BO⊥AC，
又平面AA₁C₁C⊥平面ABC，所以A₁O⊥OB．
建立如图所示的坐标系O-xyz，则A（0，-1，0），B（1，0，0），
A₁（0，0，

3

），C（0，1，0）．
（1）∵

A1B

=（1，0，-

3

），

A1C1

=

AC

=（0，2，0）
∴

A1B

•

A1C1

=0
∴A₁B⊥A₁C₁．
（2）设

m

=（x，y，z）为面BCC₁的一个法向量．
∵

BC

=（-1，1，0），

CC1

=

AA1

=（0，1，

3

）
又

m

•

BC

=

m

•

CC1

=0，
∴

-x+y=0 y+ 3 z=0

取n=（

3

，

3

，-1）．
又

n

=（1，0，0）是面ACC₁的法向量，
∴cos＜

m

，

n

＞=

m • n

| m || n |

=

3

7

=

21

7

．
由点B在平面ACC₁内的射影O在二面角的面ACC₁内，知二面角A-CC₁-B为锐角，
∴二面角A-CC₁-B的大小为arccos

21

7

．
（3）设球心为O₁，因为O是△ABC的外心，A₁O⊥平面ABC，
所以点O₁在A₁O上，则O₁是正三角形A₁AC的中心．
则球半径R=

3

3

A₁A=

2 3

3

，球表面积S=4πR²=

16

3

π．

点评：本题主要考察了利用空间向量证明线线垂直、求二面角以及求球的表面积，属常考题，较难．解题的关键是正确建立空间直角坐标系然后将线线垂直、二面角问题转化为证明向量垂直，法向量的夹角问题，同时还要求计算一定要准确！