
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | -$\frac{2}{3}$ | D. | -$\frac{3}{2}$ |
分析 由已知结合等比数列的性质列式求得a1,a4的值得答案.
解答 解:由${a_{{1_{\;}}}}+{a_4}=5,{a_2}•{a_3}$=6,
得$\left\{\begin{array}{l}{{a}_{1}+{a}_{4}=5}\\{{a}_{1}•{a}_{4}=6}\end{array}\right.$,解得$\left\{\begin{array}{l}{{a}_{1}=2}\\{{a}_{4}=3}\end{array}\right.$或$\left\{\begin{array}{l}{{a}_{1}=3}\\{{a}_{4}=2}\end{array}\right.$.
∵数列{an}单调递增,∴$\left\{\begin{array}{l}{{a}_{1}=2}\\{{a}_{4}=3}\end{array}\right.$,
则$\frac{a_4}{a_1}$=$\frac{3}{2}$.
故选:B.
点评 本题考查等比数列的通项公式,考查了等比数列的性质,是基础的计算题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
| 井号I | 1 | 2 | 3 | 4 | 5 | 6 |
| 坐标(x,y)(km) | (2,30) | (4,40) | (5,60) | (6,50) | (8,70) | (1,y) |
| 钻探深度(km) | 2 | 4 | 5 | 6 | 8 | 10 |
| 出油量(L) | 40 | 70 | 110 | 90 | 160 | 205 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
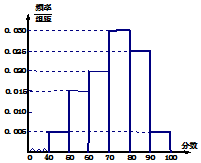 某校从高三年级期末考试的学生中抽出20名学生,其成绩(均为整数)的频率分布直方图如图所示:
某校从高三年级期末考试的学生中抽出20名学生,其成绩(均为整数)的频率分布直方图如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1或4 | C. | 4 | D. | 1或2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com