
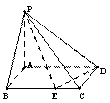
在四棱锥P-ABCD中,PA⊥底面ABCD,底面四边形ABCD是矩形,且AD=3AB,点
E是底面的边BC上的动点,设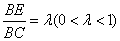 ,则满足
,则满足
PE⊥DE的λ值有
(A) 0个 (B)1个 (C)2个 (D)3个
 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
如图,AB是圆O的直径,点C是圆O上不同于A、B的一点,∠BAC=45°,点V是圆O所在平面外一点,且VA=VB=VC,E是AC的中点.
(Ⅰ)求证:OE∥平面VBC;
(Ⅱ)求证:VO 面ABC;
面ABC;
(Ⅲ)已知 是平面VBC与平面VOE所形成的二面角的平面角,且0°
是平面VBC与平面VOE所形成的二面角的平面角,且0° 90°,若OA=OV=1,求
90°,若OA=OV=1,求 的值.
的值.

查看答案和解析>>
科目:高中数学 来源: 题型:
某市实行机动车摇号购车政策,规定每年购车指标为24万个,设2014年初全市汽车保有量为500万辆,假设每年淘汰的旧车为该年初汽车保有量的4%,每年新购车辆数等于该年购车指标.
(Ⅰ)求2015年初和2016年初全市汽车保有量(万辆);
(Ⅱ)设2014年初的汽车保有量为 ,
,  年后汽车保有量为
年后汽车保有量为 ,求证:数列
,求证:数列 为等比数列;
为等比数列;
(Ⅲ)要想将全市每年的汽车保有量控制在550万辆以下,是否需要调整每年的购车指标,若不需调整,说明理由,若需调整,求出每年购车指标的最大值(万个).
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在四棱锥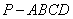 中,底面
中,底面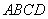 是边长为
是边长为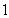 的正方形,
的正方形,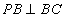 ,
,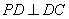 ,且
,且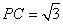 .
.
(Ⅰ)求证: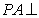 平面
平面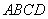 ;
;
(Ⅱ)求二面角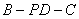 的余弦值;
的余弦值;
(Ⅲ)棱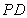 上是否存在一点
上是否存在一点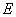 ,使直线
,使直线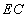 与平面
与平面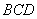 所成的角是
所成的角是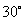 ?若存在,求
?若存在,求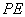 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知集合,对于数列中.
(Ⅰ)若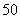 项数列
项数列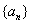 满足
满足 ,
, ,则数列
,则数列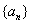 中有多少项取值为零?(
中有多少项取值为零?(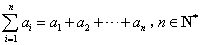 )
)
(Ⅱ)若各项非零数列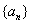 和新数列
和新数列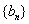 满足
满足 ().
().
(ⅰ)若首项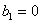 ,末项
,末项 ,求证数列
,求证数列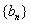 是等差数列;
是等差数列;
(ⅱ)若首项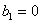 ,末项
,末项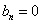 ,记数列
,记数列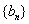 的前
的前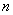 项和为
项和为 ,求
,求 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com