
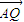 =��
=��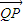 ���ˣ�0������̽����ֱ��OQ��ƽ��PBD���ɽǵĴ�С�Ƿ�һ������
���ˣ�0������̽����ֱ��OQ��ƽ��PBD���ɽǵĴ�С�Ƿ�һ������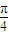 ����˵�����ɣ�
����˵�����ɣ�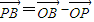 =�� 2
=�� 2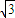 -x��2��-x�����Ӷ�ȷ��PB����Сֵ�������ɵ�����P-BDEF�������
-x��2��-x�����Ӷ�ȷ��PB����Сֵ�������ɵ�����P-BDEF�������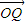 �����꣬���ƽ��PBD�ķ�����
�����꣬���ƽ��PBD�ķ�����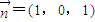 �����������ļнǹ�ʽ����ֱ��OQ��ƽ��PBD���ɵĽǣ��Ӷ��ɵý��۳�����
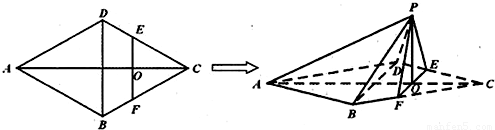
�����������ļнǹ�ʽ����ֱ��OQ��ƽ��PBD���ɵĽǣ��Ӷ��ɵý��۳�����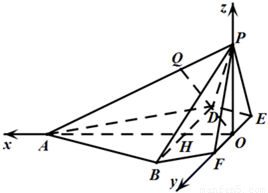 ����֤����������ABCD�ĶԽ����ഹֱ��
����֤����������ABCD�ĶԽ����ഹֱ�� ��
��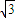 -x��OA=4
-x��OA=4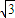 -x��
-x��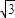 -x��2��0����
-x��2��0����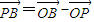 =�� 2
=�� 2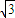 -x��2��-x������6�֣�
-x��2��-x������6�֣�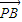 |=
|=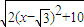 ��
��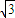 ʱ��|PB|min=
ʱ��|PB|min=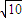 ��
��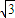 ��OH=
��OH= ��7�֣�
��7�֣�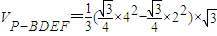 =3����8�֣�
=3����8�֣�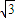 ����A��3
����A��3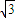 ��0��0����B��
��0��0����B��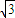 ��2��0����D��
��2��0����D��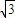 ��-2��0����P��0��0��
��-2��0����P��0��0��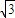 ����
����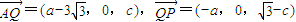 ����9�֣�
����9�֣�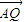 =��
=��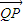 ���ˣ�0����
���ˣ�0����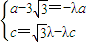 ����
����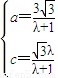 ��
��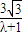 ��
��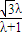 ����
����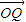 =��
=��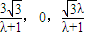 ���� ��10�֣�
���� ��10�֣�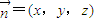 ����
����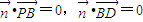 ��
��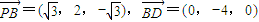 ����
����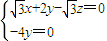 ��
��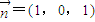 ����11�֣�
����11�֣� |=
|=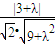 =
=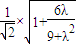 ����12�֣�
����12�֣�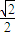 ����13�֣�
����13�֣�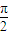 ]����ȣ�
]����ȣ� ��
�� �������۳����� ��14�֣�
�������۳����� ��14�֣�


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| AQ |
| QP |

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| V1 |
| V2 |
| 4 |
| 3 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com