
【题目】在如图所示的多面体ABCDEF中,四边形ABCD为正方形,底面ABFE为直角梯形,∠ABF为直角, ![]() ,平面ABCD⊥平面ABFE.
,平面ABCD⊥平面ABFE.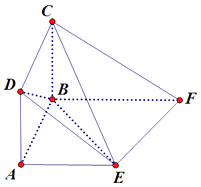
(1)求证:DB⊥EC;
(2)若AE=AB,求二面角C﹣EF﹣B的余弦值.
【答案】
(1)证明:∵底面ABFE为直角梯形,AE∥BF,∠EAB=90°,
∴AE⊥AB,BF⊥AB,
∵平面ABCD⊥平面ABFE,平面ABCD∩平面ABFE=AB,
∴AE⊥平面ABCD.BF⊥平面ABCD,∴BF⊥BC,
设AE=t,以BA,BF,BC所在的直线分别为x,y,z轴建立如图坐标系,

则B(0,0,0),C(0,0,1),D(1,0,1),E(1,t,0) ![]()
∵ ![]() =0,∴DB⊥EC.
=0,∴DB⊥EC.
(2)解:由(1)知 ![]() 是平面BEF的一个法向量,
是平面BEF的一个法向量,
设 ![]() =(x,y,z)是平面CEF的一个法向量,
=(x,y,z)是平面CEF的一个法向量,
AE=AB=1,E(1,1,0),F(0,2,0),
∴ ![]() =(1,1,﹣1),
=(1,1,﹣1), ![]() =(0,2,﹣1),
=(0,2,﹣1),
则  ,取z=2,
,取z=2, ![]() =(1,1,2),
=(1,1,2),
∴cos< ![]() >=
>=  =
= ![]() ,
,
即二面角C﹣EF﹣B的余弦值为 ![]() .
.
【解析】本题抓住在多面体ABCDEF上建立坐标,建立坐标一定要满足两两相互垂直,建立好坐标求出相关点对应的坐标,根据空间向量知识解出本题。注意理解二面角及其求法。
【考点精析】解答此题的关键在于理解直线与平面垂直的性质的相关知识,掌握垂直于同一个平面的两条直线平行.


科目:高中数学 来源: 题型:
【题目】极坐标系的极点为直角坐标系的原点,极轴为x轴的正半轴,两坐标系中的单位长度相同,已知曲线C的极坐标方程为ρ=2(sinθ+cosθ).
(Ⅰ)求C的直角坐标方程;
(Ⅱ)直线 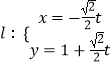 (t为参数)与曲线C交于A,B两点,与y轴交于E,求|EA|+|EB|的值.
(t为参数)与曲线C交于A,B两点,与y轴交于E,求|EA|+|EB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=xex﹣ax(a∈R,a为常数),e为自然对数的底数.
(1)若函数f(x)的任意一条切线都不与y轴垂直,求a的取值范围;
(2)当a=2时,求使得f(x)+k>0成立的最小正整数k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在空间直角坐标系O﹣xyz中,已知A(2,0,0),B(0,2,0),C(0,0,0),P(0,1, ![]() ),则三棱锥P﹣ABC在坐标平面xOz上的正投影图形的面积为;该三棱锥的最长棱的棱长为 .
),则三棱锥P﹣ABC在坐标平面xOz上的正投影图形的面积为;该三棱锥的最长棱的棱长为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合U={1,2,…,100},TU.对数列{an}(n∈N*),规定:
①若T=,则ST=0;
②若T={n1 , n2 , …,nk},则ST=a ![]() +a
+a ![]() +…+a
+…+a ![]() .
.
例如:当an=2n,T={1,3,5}时,ST=a1+a3+a5=2+6+10=18.
已知等比数列{an}(n∈N*),a1=1,且当T={2,3}时,ST=12,求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代名著《庄子天下篇》中有一句名言“一尺之棰,日取其半,万世不竭”,其意思为:一尺的木棍,每天截取一半,永远都截不完,现将该木棍依此规律截取,如图所示的程序框图的功能就是计算截取7天后所剩木棍的长度(单位:尺),则①②③处可分别填入的是( )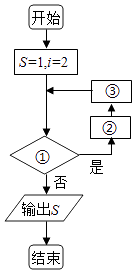
A.①i≤7?②s=s﹣ ![]() ③i=i+1
③i=i+1
B.①i≤128?②s=s﹣ ![]() ③i=2i
③i=2i
C.①i≤7?②s=s﹣ ![]() ③i=i+1
③i=i+1
D.①i≤128?②s=s﹣ ![]() ③i=2i
③i=2i
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线C的极坐标方程为ρ=2cosθ+2sinθ(0≤θ<2π),点M(1, ![]() ),以极点O为原点,以极轴为x轴的正半轴建立平面直角坐标系.已知直线l:
),以极点O为原点,以极轴为x轴的正半轴建立平面直角坐标系.已知直线l: 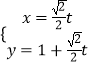 (t为参数)与曲线C交于A,B两点,且|MA|>|MB|.
(t为参数)与曲线C交于A,B两点,且|MA|>|MB|.
(1)若P(ρ,θ)为曲线C上任意一点,求ρ的最大值,并求此时点P的极坐标;
(2)求 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】候鸟每年都要随季节的变化而进行大规模地迁徙,研究某种鸟类的专家发现,该种鸟类的飞行速度v(单位:m/s)与其耗氧量Q之间的关系为:v=a+blog3 ![]() (其中a,b是实数).据统计,该种鸟类在静止的时候其耗氧量为30个单位,而其耗氧量为90个单位时,其飞行速度为1 m/s.
(其中a,b是实数).据统计,该种鸟类在静止的时候其耗氧量为30个单位,而其耗氧量为90个单位时,其飞行速度为1 m/s.
(1)求出a,b的值;
(2)若这种鸟类为赶路程,飞行的速度不能低于2 m/s,则其耗氧量至少要多少个单位?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com