
【题目】已知函数 ![]() ,若
,若 ![]() ,且
,且 ![]() 对任意的
对任意的 ![]() 恒成立,则
恒成立,则 ![]() 的最大值为( )
的最大值为( )
A.2
B.3
C.4
D.5
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面ABCD是平行四边形,侧面PAD是边长为2的正三角形,AB=BD= ![]() ,PB=3.
,PB=3.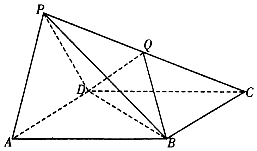
(1)求证:平面PAD⊥平面ABCD;
(2)设Q是棱PC上的点,当PA∥平面BDQ时,求二面角A﹣BD﹣Q的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的多面体ABCDEF中,四边形ABCD为正方形,底面ABFE为直角梯形,∠ABF为直角, ![]() ,平面ABCD⊥平面ABFE.
,平面ABCD⊥平面ABFE.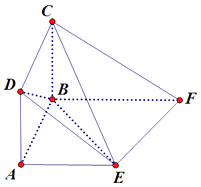
(1)求证:DB⊥EC;
(2)若AE=AB,求二面角C﹣EF﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C所对的边分别为a,b,c,若sinA=cos( ![]() ﹣B),a=3,c=2.
﹣B),a=3,c=2.
(1)求 ![]() 的值;
的值;
(2)求tan( ![]() ﹣B)的值.
﹣B)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.若p∨q为真命题,则p∧q为真命题
B.“a>0,b>0”是“ ![]() ≥2”的充要条件
≥2”的充要条件
C.命题“若x2-3x+2=0,则x=1或x=2”的逆否命题为“若x≠1或x≠2,则x2-3x+2≠0”
D.命题p:x∈R,x2+x-1<0,则﹁p:x∈R,x2+x-1≥0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系 ![]() 中,曲线
中,曲线 ![]() 的参数方程为
的参数方程为 ![]() (
( ![]() 为参数),在以
为参数),在以 ![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线 ![]() 是圆心为
是圆心为 ![]() ,半径为1的圆.
,半径为1的圆.
(1)求曲线 ![]() ,
, ![]() 的直角坐标方程;
的直角坐标方程;
(2)设 ![]() 为曲线
为曲线 ![]() 上的点,
上的点, ![]() 为曲线
为曲线 ![]() 上的点,求
上的点,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①x∈R,不等式x2+2x>4x-3均成立;
②若log2x+logx2≥2,则x>1;
③“若a>b>0且c<0,则 ![]() ”的逆否命题;
”的逆否命题;
④若p且q为假命题,则p,q均为假命题.
其中真命题是( )
A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在吸烟与患肺癌这两个分类变量的独立性检验的计算中,下列说法正确的是( )
A.若 ![]() 的观测值为
的观测值为 ![]() ,在犯错误的概率不超过
,在犯错误的概率不超过 ![]() 的前提下认为吸烟与患肺癌有关系,那么在100个吸烟的人中必有99人患有肺癌.
的前提下认为吸烟与患肺癌有关系,那么在100个吸烟的人中必有99人患有肺癌.
B.由独立性检验可知,在犯错误的概率不超过 ![]() 的前提下认为吸烟与患肺癌有关系时,我们说某人吸烟,那么他有
的前提下认为吸烟与患肺癌有关系时,我们说某人吸烟,那么他有 ![]() 的可能患有肺癌.
的可能患有肺癌.
C.若从统计量中求出在犯错误的概率不超过 ![]() 的前提下认为吸烟与患肺癌有关系,是指有
的前提下认为吸烟与患肺癌有关系,是指有 ![]() 的可能性使得判断出现错误.
的可能性使得判断出现错误.
D.以上三种说法都不正确.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com