
【题目】如图,四棱锥P﹣ABCD的底面ABCD是平行四边形,侧面PAD是边长为2的正三角形,AB=BD= ![]() ,PB=3.
,PB=3.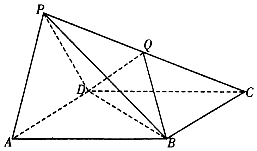
(1)求证:平面PAD⊥平面ABCD;
(2)设Q是棱PC上的点,当PA∥平面BDQ时,求二面角A﹣BD﹣Q的余弦值.
【答案】
(1)解:取AD中点O,连结OP,OB,
∵△PAD是边长为2的正三角形,∴OP= ![]() ,OP⊥AD,
,OP⊥AD,
又AB=AD= ![]() ,∴OB⊥AD,且OB=
,∴OB⊥AD,且OB= ![]() .
.
于是OB2+OP2=9=PB2,从而OP⊥OB.
所以OP⊥面ABCD,而OP面PAD,所以面PAD⊥面ABCD.
(2)连结AC交BD于E,则E为AC的中点,连结EQ,当PA∥面BDQ时,PA∥EQ,所以Q是BC中点.
由(1)知OA,OB,OP两两垂直,分别以OA,OB,OP所在直线为x,y,z轴建立空间直角坐标系,
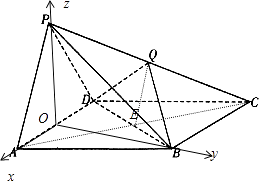
则B(0, ![]() ,0),C(﹣2,
,0),C(﹣2, ![]() ,0),D(﹣1,0,0),P(0,0,
,0),D(﹣1,0,0),P(0,0, ![]() ),Q(﹣1,
),Q(﹣1, ![]() ),
),
![]() ,
, ![]() .
.
设面BDQ的法向量为 ![]() ,由
,由 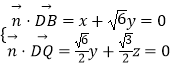 ,取
,取 ![]() .
.
面ABD的法向量是 ![]() ,∴cos<
,∴cos< ![]() >=﹣
>=﹣ ![]() .
.
∵二面角A﹣BD﹣Q是钝角,∴二面角A﹣BD﹣Q的余弦值为﹣ ![]() .
.
【解析】(1)取AD中点O,连结OP,OB,根据等边三角形三线合一可证OP⊥AD,由几何关系得出各线段长度后结合勾股定理证出OP⊥OB,由线面垂直得到面面垂直,(2)以O为坐标原点,以OA,OB,OP所在直线为x,y,z轴建立空间直角坐标系,由法向量得到二面角的余弦值.
【考点精析】本题主要考查了平面与平面垂直的判定的相关知识点,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】极坐标系的极点为直角坐标系的原点,极轴为x轴的正半轴,两坐标系中的单位长度相同,已知曲线C的极坐标方程为ρ=2(sinθ+cosθ).
(Ⅰ)求C的直角坐标方程;
(Ⅱ)直线 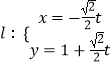 (t为参数)与曲线C交于A,B两点,与y轴交于E,求|EA|+|EB|的值.
(t为参数)与曲线C交于A,B两点,与y轴交于E,求|EA|+|EB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的参数方程为 ![]() (φ为参数),以原点为极点,x轴的非负半轴为极轴建立极坐标系.
(φ为参数),以原点为极点,x轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求曲线C的极坐标方程;
(Ⅱ)已知倾斜角为135°且过点P(1,2)的直线l与曲线C交于M,N两点,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南宋时期的数学家秦九韶在他的著作《数书九章》中提出了计算多项式f(x)=anxn+an﹣1xn﹣1+…+a1x+a0的值的秦九韶算法,即将f(x)改写成如下形式:f(x)=(…((anx+an﹣1)x+an﹣2)x+…+a1)x+a0 , 首先计算最内层一次多项式的值,然后由内向外逐层计算一次多项式的值,这种算法至今仍是比较先进的算法,将秦九韶算法用程序框图表示如图,则在空白的执行框内应填入( )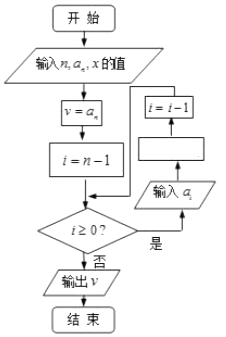
A.v=vx+ai
B.v=v(x+ai)
C.v=aix+v
D.v=ai(x+v)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f'(x)=2x+m,且f(0)=0,函数f(x)的图象在点A(1,f(1))处的切线的斜率为3,数列 ![]() 的前n项和为Sn , 则S2017的值为( )
的前n项和为Sn , 则S2017的值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=xex﹣ax(a∈R,a为常数),e为自然对数的底数.
(1)若函数f(x)的任意一条切线都不与y轴垂直,求a的取值范围;
(2)当a=2时,求使得f(x)+k>0成立的最小正整数k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在空间直角坐标系O﹣xyz中,已知A(2,0,0),B(0,2,0),C(0,0,0),P(0,1, ![]() ),则三棱锥P﹣ABC在坐标平面xOz上的正投影图形的面积为;该三棱锥的最长棱的棱长为 .
),则三棱锥P﹣ABC在坐标平面xOz上的正投影图形的面积为;该三棱锥的最长棱的棱长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com