
【题目】如图,在正方形ABCD中,E为AB的中点,P为以A为圆心、AB为半径的圆弧上的任意一点,设向量 ![]() ,则λ+μ的最小值为 .
,则λ+μ的最小值为 . 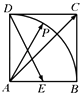
【答案】![]()
【解析】解:以A为原点,以AB所在的为x轴,建立坐标系,设正方形ABCD的边长为1,
则E( ![]() ,0),C(1,1),D(0,1),A(0,0),B(1,0).
,0),C(1,1),D(0,1),A(0,0),B(1,0).
设 P(cosθ,sinθ),∴ ![]() =(1,1).
=(1,1).
再由向量 ![]() =λ(
=λ( ![]() ,﹣1)+μ(cosθ,sinθ)=(
,﹣1)+μ(cosθ,sinθ)=( ![]() ,﹣λ+μsinθ )=(1,1),
,﹣λ+μsinθ )=(1,1),
∴ 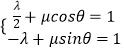 ,∴
,∴ 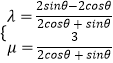 ,
,
∴λ+μ= ![]() =
= ![]() =﹣1+
=﹣1+ ![]() .
.
由题意得 0≤θ≤ ![]() ,∴0≤cosθ≤1,0≤sinθ≤1.
,∴0≤cosθ≤1,0≤sinθ≤1.
求得(λ+μ)′= ![]() =
= ![]() >0,
>0,
故λ+μ在[0, ![]() ]上是增函数,故当θ=0时,即cosθ=1,这时λ+μ取最小值为
]上是增函数,故当θ=0时,即cosθ=1,这时λ+μ取最小值为 ![]() =
= ![]() ,
,
故答案为: ![]() .
.
以A为原点,AB为x轴,AD为y轴建立平面直角坐标系,表示出各点坐标,设P(cosθ,sinθ),由向量运算得出λ+μ的解析式,求导并在给定区间得出最值.


科目:高中数学 来源: 题型:
【题目】如图,在平面四边形ABCD中,已知∠A= ![]() ,∠B=
,∠B= ![]() ,AB=6.在AB边上取点E使得BE=1,连结EC,ED,若∠CED=
,AB=6.在AB边上取点E使得BE=1,连结EC,ED,若∠CED= ![]() ,EC=
,EC= ![]() .则CD= .
.则CD= . 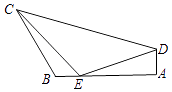
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的首项a1=m,其前n项和为Sn , 且满足Sn+Sn+1=3n2+2n,若对n∈N+ , an<an+1恒成立,则m的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数h(x)=﹣|x﹣3|.
(1)若h(x)﹣|x﹣2|≤n对任意的x>0恒成立,求实数n的最小值;
(2)若函数f(x)= 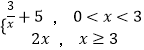 ,求函数g(x)=f(x)+h(x)的值域.
,求函数g(x)=f(x)+h(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣a+lnx.
(Ⅰ)若a=1,求证:当x>1时,f(x)>2x﹣1;
(Ⅱ)若存在x0≥e,使f(x0)<2lnx0 , 求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆G: ![]() +y2=1,与x轴不重合的直线l经过左焦点F1 , 且与椭圆G相交于A,B两点,弦AB的中点为M,直线OM与椭圆G相交于C,D两点.
+y2=1,与x轴不重合的直线l经过左焦点F1 , 且与椭圆G相交于A,B两点,弦AB的中点为M,直线OM与椭圆G相交于C,D两点.
(1)若直线l的斜率为1,求直线OM的斜率;
(2)是否存在直线l,使得|AM|2=|CM||DM|成立?若存在,求出直线l的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的多面体ABCDEF中,ABCD为直角梯形,AB∥CD,∠DAB=90°,四边形ADEF为等腰梯形,EF∥AD,已知AE⊥EC,AB=AF=EF=2,AD=CD=4.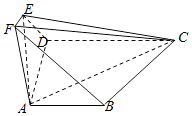
(1)求证:平面ABCD⊥平面ADEF;
(2)求直线CF与平面EAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面ABCD是平行四边形,侧面PAD是边长为2的正三角形,AB=BD= ![]() ,PB=3.
,PB=3.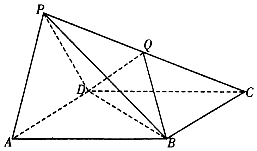
(1)求证:平面PAD⊥平面ABCD;
(2)设Q是棱PC上的点,当PA∥平面BDQ时,求二面角A﹣BD﹣Q的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com