
【题目】已知函数![]() ,
,![]() .
.
(1)设函数![]() ,讨论
,讨论![]() 的单调性;
的单调性;
(2)设函数![]() ,若
,若![]() 的图象与
的图象与![]() 的图象有
的图象有![]() ,
,![]() 两个不同的交点,证明:
两个不同的交点,证明:![]() .
.
【答案】(1)答案不唯一,具体见解析(2)证明见解析
【解析】
(1)求出![]() 的表达式并求导,分类讨论
的表达式并求导,分类讨论![]() 的单调性;(2)由题意可得
的单调性;(2)由题意可得![]() 有两个不同的根,则
有两个不同的根,则![]() ①,
①,![]() ②, 消去参数
②, 消去参数![]() 得
得![]() ,构造函数
,构造函数![]() 求导研究函数单调性并利用放缩法推出
求导研究函数单调性并利用放缩法推出![]() ,再次构造函数
,再次构造函数![]() ,通过证明
,通过证明![]() 来证明
来证明![]() .
.
(1)![]() ,定义域为
,定义域为![]() ,
,
![]() .
.
当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
当![]() 时,令
时,令![]() ,得
,得![]() ,所以
,所以![]() 在
在![]() ,
,![]() 上单调递增;
上单调递增;
令![]() ,得
,得![]() ,所以
,所以![]() 在
在![]() 上单调递减.
上单调递减.
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增.
上单调递增.
当![]() 时,令
时,令![]() ,得
,得![]() ,所以
,所以![]() 在
在![]() ,
,![]() 上单调递增;
上单调递增;
令![]() ,得
,得![]() ,所以
,所以![]() 在
在![]() 上单调递减.
上单调递减.
(2)![]() ,
,
因为函数![]() 的图象与
的图象与![]() 的图象有两个不同的交点,
的图象有两个不同的交点,
所以关于![]() 的方程
的方程![]() ,即
,即![]() 有两个不同的根.
有两个不同的根.
由题知![]() ①,
①,![]() ②,
②,
①+②得![]() ③,
③,
②-①得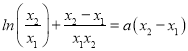 ④.
④.
由③,④得![]() ,不妨设
,不妨设![]() ,记
,记![]() .
.
令![]() ,则
,则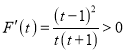 ,
,
所以![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,
,
则![]() ,即
,即![]() ,所以
,所以![]() .
.
因为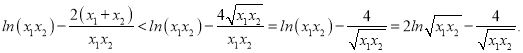
所以![]() ,即
,即![]() .
.
令![]() ,则
,则![]() 在
在![]() 上单调递增.
上单调递增.
又![]() ,所以
,所以![]() ,
,
即![]() ,所以
,所以![]() .
.
两边同时取对数可得![]() ,得证.
,得证.


科目:高中数学 来源: 题型:
【题目】如图,在边长为3的正方形ABCD中,点E,F分别在边AB,BC上(如图1),且BE=BF,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点A′(如图2).

(1)求证:A′D⊥EF;
(2)BF![]() BC时,求点A′到平面DEF的距离.
BC时,求点A′到平面DEF的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年初,我国突发新冠肺炎疫情.面对“突发灾难”,举国上下心,继解放军医疗队于除夕夜飞抵武汉,各省医疗队也陆续增援,纷纷投身疫情防控与病人救治之中.为分担“逆行者”的后顾之忧,某大学学生志愿者团队开展“爱心辅学”活动,为抗疫前线工作者子女在线辅导功课.现随机安排甲、乙、丙3名志愿者为某学生辅导数学、物理、化学、生物4门学科,每名志愿者至少辅导1门学科,每门学科由1名志愿者辅导,则数学学科恰好由甲辅导的概率为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,则称区间
,则称区间![]() 是函数
是函数![]() 的“完美区间”,另外,定义区间
的“完美区间”,另外,定义区间![]() 的“复区间长度”为
的“复区间长度”为![]() ,已知函数
,已知函数![]() ,则( )
,则( )
A.![]() 是
是![]() 的一个“完美区间”
的一个“完美区间”
B. 是
是![]() 的一个“完美区间”
的一个“完美区间”
C.![]() 的所有“完美区间”的“复区间长度”的和为
的所有“完美区间”的“复区间长度”的和为![]()
D.![]() 的所有“完美区间”的“复区间长度”的和为
的所有“完美区间”的“复区间长度”的和为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】生男生女都一样,女儿也是传后人.由于某些地区仍然存在封建传统思想,头胎的男女情况可能会影响生二孩的意愿,现随机抽取某地200户家庭进行调查统计.这200户家庭中,头胎为女孩的频率为0.5,生二孩的频率为0.525,其中头胎生女孩且生二孩的家庭数为60.
(1)完成下列![]() 列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
生二孩 | 不生二孩 | 合计 | |
头胎为女孩 | 60 | ||
头胎为男孩 | |||
合计 | 200 |
(2)在抽取的200户家庭的样本中,按照分层抽样的方法在生二孩的家庭中抽取了7户,进一步了解情况,在抽取的7户中再随机抽取4户,求抽到的头胎是女孩的家庭户数![]() 的分布列及数学期望.
的分布列及数学期望.
附:
| 0.15 | 0.05 | 0.01 | 0.001 |
| 2.072 | 3.841 | 6.635 | 10.828 |
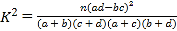 (其中
(其中![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() 轴,直线
轴,直线![]() 交
交![]() 轴于
轴于![]() 点,
点,![]() ,
,![]() 为椭圆
为椭圆![]() 上的动点,
上的动点,![]() 的面积的最大值为1.
的面积的最大值为1.
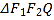
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作两条直线与椭圆
作两条直线与椭圆![]() 分别交于
分别交于![]() 且使
且使![]() 轴,如图,问四边形
轴,如图,问四边形![]() 的两条对角线的交点是否为定点?若是,求出定点的坐标;若不是,请说明理由.
的两条对角线的交点是否为定点?若是,求出定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】马林●梅森是17世纪法国著名的数学家和修道士,也是当时欧洲科学界一位独特的中心人物,梅森在欧几里得、费马等人研究的基础上对2p﹣1作了大量的计算、验证工作,人们为了纪念梅森在数论方面的这一贡献,将形如2P﹣1(其中p是素数)的素数,称为梅森素数.若执行如图所示的程序框图,则输出的梅森素数的个数是( )
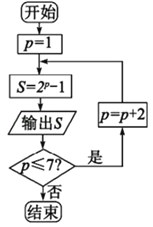
A.3B.4C.5D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,离心率为
,离心率为![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() ,
,![]() ,
,![]() 为椭圆
为椭圆![]() 上的三点,
上的三点,![]() 与
与![]() 交于点
交于点![]() ,且
,且![]() ,当
,当![]() 的中点恰为点
的中点恰为点![]() 时,判断
时,判断![]() 的面积是否为常数,并说明理由.
的面积是否为常数,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com