解:(I)由已知,得2f(x+2)=f(x),
∴f(x)=2f(x+2)=4f(x+4)(4分)
∵x∈(0,2)时,f(x)=lnx+ax,
设x∈(-4,-2),则x+4∈(0,2),
∴f(x+4)=ln(x+4)+a(x+4),
∴x∈(-4,-2)时,f(x)=4f(x+4)=4ln(x+4)+4a(x+4),
所以

,
∵x∈(-4,-2),
∴-4ax<4+16a,
∵
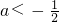
,
∴

.
又由
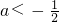
,可得

,
∴f(x)在

上是增函数,在

上是减函数,
∴

.
∴a=-1(7分)
(II)设f(x)的值域为A,g(x)的值域为B,
则由已知,对于任意的x
1∈(1,2),总存在x
2∈(1,2),使f(x
1)-g(x
2)=0得,A⊆B.(9分)
由(I)a=-1,当x∈(1,2)时,f(x)=lnx-x,
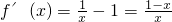
,
∵x∈(1,2),
∴f′(x)<0,f(x)在x∈(1,2)上单调递减函数,
∴f(x)的值域为A=(ln2-2,-1)(10分)
∵g'(x)=bx
2-b=b(x-1)(x+1),
∴(1)当b<0时,g(x)在(1,2)上是减函数,
此时,g(x)的值域为

,
为满足A⊆B,又

∴

即

.(11分)
(2)当b>0时,g(x)在(1,2)上是单调递增函数,
此时,g(x)的值域为

,为满足A⊆B,
又,∴

,
∴

,
综上可知b的取值范围是

(12分)
分析:(I)先求出函数在(-4,-2)上的解析式,利用函数的导数求出函数的最大值(用a表示),令其等于-4,从而求出a;
(II)由任意的x
1∈(1,2),总存在x
2∈(1,2),使f(x
1)-g(x
2)=0,函数f(x)的值域是函数g(x)值域的子集,即转化为求两个函数的值域,用函数的导数法即可解决.
点评:本题考查函数的导数在研究函数的最值中的应用,考查子集概念的理解,解题的关键是分类讨论思想与转化思想,化“生”为“熟”是解题之“良方”.

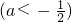 ,当x∈(-4,-2)时,f(x)的最大值为-4.
,当x∈(-4,-2)时,f(x)的最大值为-4.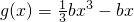 ,x∈(1,2).若对任意的x1∈(1,2),总存在x2∈(1,2),使f(x1)-g(x2)=0,求实数b的取值范围.
,x∈(1,2).若对任意的x1∈(1,2),总存在x2∈(1,2),使f(x1)-g(x2)=0,求实数b的取值范围. ,
,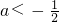 ,
, .
.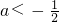 ,可得
,可得 ,
, 上是增函数,在
上是增函数,在 上是减函数,
上是减函数, .
.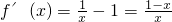 ,
, ,
,
 即
即 .(11分)
.(11分) ,为满足A⊆B,
,为满足A⊆B, ,
, ,
, (12分)
(12分)
