
(拓展深化)如图①所示,△ABC内接于⊙O,AB=AC,D是BC边上的一点,E是直线AD和△ABC外接圆的交点.
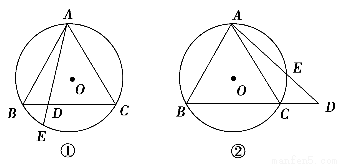
(1)求证:AB2=AD·AE;
(2)如图②所示,当D为BC延长线上的一点时,第(1)题的结论成立吗?若成立,请证明;若不成立,请说明理由.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2013-2014学年高中数学人教A版选修4-1达标检测第2讲练习卷(解析版) 题型:选择题
如图所示,PA切圆于A,PA=8,直线PCB交圆于C、B,连接AB、AC,且PC=4,AD⊥BC于D,∠ABC=α,∠ACB=β,则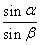 的值等于
的值等于

A.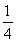 B.
B. C.2 D.4
C.2 D.4
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高中数学人教A版选修4-1知能达标2-4练习卷(解析版) 题型:解答题
(拓展深化)如图所示,△ABC内接于⊙O,AB=AC,直线XY切⊙O于点C,BD∥XY,AC、BD相交于E.

(1)求证:△ABE≌△ACD;
(2)若AB=6 cm,BC=4 cm,求AE的长.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高中数学人教A版选修4-1知能达标2-3练习卷(解析版) 题型:选择题
已知圆的半径为6.5 cm,圆心到直线l的距离为4.5 cm,那么这条直线和这个圆的公共点的个数是
A.0 B.1 C.2 D.不能确定
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高中数学人教A版选修4-1知能达标2-2练习卷(解析版) 题型:填空题
若BE和CF是△ABC的边AC和AB边上的高,则________四点共圆.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高中数学人教A版选修4-1知能达标2-1练习卷(解析版) 题型:选择题
如图所示,若圆内接四边形的对角线相交于E,则图中相似三角形有( ).

A.1对 B.2对
C.3对 D.4对
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高中数学人教A版选修4-1知能达标1-4练习卷(解析版) 题型:填空题
在Rt△ABC中,∠C=90°,a-b=1,tan A=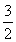 ,其中a、b分别是∠A和∠B的对边,则斜边上的高h=________.
,其中a、b分别是∠A和∠B的对边,则斜边上的高h=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高中数学人教A版选修4-1知能达标1-2练习卷(解析版) 题型:解答题
如图所示,在△ABC中,AE∶EB=1∶3,BD∶DC=2∶1,AD与CE相交于F,求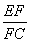 +
+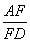 的值.
的值.
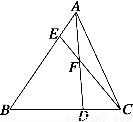
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西西安第一中学高三第二学期第二次模拟考试文科数学试卷(解析版) 题型:解答题
设函数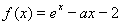 .
.
(1)求函数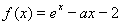 的图像在点
的图像在点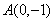 处的切线方程;
处的切线方程;
(2)求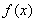 的单调区间;
的单调区间;
(3)若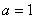 ,
,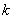 为整数,且当
为整数,且当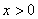 时,
时,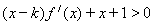 ,求
,求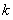 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com