
分析 根据题意,构造函数g(x)=x3f(x),x∈(-∞,0),利用导数判断g(x)的单调性,
再把不等式(x+2015)3f(x+2015)+27f(-3)>0化为g(x+2015)>g(-3),
利用单调性求出不等式的解集.
解答 解:根据题意,令g(x)=x3f(x),
其导函数为g′(x)=3x2f(x)+x3f′(x)=x2[3f(x)+xf′(x)],
∵x∈(-∞,0)时,3f(x)+xf′(x)>0,
∴g(x)>0,
∴g(x)在(-∞,0)上单调递增;
又不等式(x+2015)3f(x+2015)+27f(-3)>0可化为
(x+2015)3f(x+2015)>(-3)3f(-3),
即g(x+2015)>g(-3),
∴0>x+2015>-3;
解得-2015>x>-2018,
∴该不等式的解集是为(-2018,-2015).
故答案为:(-2018,-2015).
点评 本题考查了利用导数研究函数的单调性问题,也考查了利用函数的单调性求不等式的解集的问题,是综合性题目.


科目:高中数学 来源: 题型:选择题
| A. | 3$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -2 | C. | -4 | D. | -8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 19 | B. | $\frac{19}{14}$ | C. | -$\frac{8}{7}$ | D. | $\frac{8}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
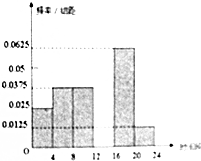 上饶市政府为缓解城市交通压力,计划对金龙岗路等交通要道由双向通行改为单项通行,为调查金龙岗路的通行能力,交警部门将某一天24小时分为六个时段,分别是[0,4)…[20,24)(小时),并记录每一时段通行此路的机动车的辆数,共计为600辆,绘制如下部分频率分布直方图,观察图形的信息,回答下列问题:
上饶市政府为缓解城市交通压力,计划对金龙岗路等交通要道由双向通行改为单项通行,为调查金龙岗路的通行能力,交警部门将某一天24小时分为六个时段,分别是[0,4)…[20,24)(小时),并记录每一时段通行此路的机动车的辆数,共计为600辆,绘制如下部分频率分布直方图,观察图形的信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com