练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．已知M（a，5-a，2a-1），N（1，a+2，2-a）两点，当|MN|取得最小值时，a的值是（　　）
    A．19B．$\frac{19}{14}$C．-$\frac{8}{7}$D．$\frac{8}{7}$

    分析 利用空间零点的距离公式以及二次函数的性质求解距离的最值即可．

    解答 解：M（a，5-a，2a-1），N（1，a+2，2-a）两点，
    |MN|=$\sqrt{（a-1）^{2}+（5-a-a-2）^{2}+（2a-1-2+a）^{2}}$=$\sqrt{14{a}^{2}-32a+19}$=$\sqrt{14（{a-\frac{8}{7}）}^{2}+\frac{5}{7}}$≥$\frac{\sqrt{35}}{7}$，当且仅当a=$\frac{8}{7}$取等号．
    故选：D．

    点评 本题考查空间距离公式的应用，二次函数的最值，考查计算能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    14．已知定义在R上的奇函数f（x）满足f（x+2）=-f（x），且f（1）=2，则f（2015）的值为（　　）
    A．2B．0C．-2D．-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

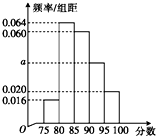    15．某高校在某年的自主招生考试成绩中随机抽取50名学生的笔试成绩，绘制成频率分布直方图如图所示，若要从成绩在[85，90），[90，95），[95，100]三组内的学生中，用分层抽样的方法抽取12人参加面试，则成绩在[90，100]内的学生应抽取的人数为6．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．设Sn是等差数列{an}的前n项和，S6≥21且S15≤120，则a10的最大值是10．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．设函数f（x）是定义在（-∞，0）上的可导函数，其导函数为f′（x），且有3f（x）+xf′（x）＞0，则不等式（x+2015）3f（x+2015）+27f（-3）＞0的解集是（-2018，-2015）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

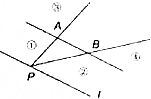    9．如图，点P是直线l上一点，l∥直线AB，如果存在实数x，y，使得$\overrightarrow{PC}=x\overrightarrow{PA}+y\overrightarrow{PB}$，且x+y=2，x＞2，则点C所在的区域是图中标示的区域（　　）
    A．①B．②C．③D．④

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．设a1，a2，…an是正整数1，2，3，…，n的一个排列，令bj表示排在j的左边且比j大的数的个数，称为j的逆序数．如在排列3，5，1，4，2，6中，5的逆序数是0，2的逆序数是3，则由1至8这8个数字构成的所有排列中，满足1的逆序数是2，2的逆序数是3，5的逆序数是3的不同排列种数是（　　）
    A．144B．172C．180D．192

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．下列说法中正确的序号为（　　）
    A．若直线l平行于平面α内的无数条直线，则l∥α；
    B．若α∥β，a?α，b?β，则a与b是异面直线；
    C．若α∥β，a?α，则a∥β；
    D．若α∩β=b，a?α，则a与β一定相交．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．函数f（x）=$\frac{1}{2}$x-cosx在区间[0，2π]上的值域为$[-1，\frac{7π}{12}+\frac{\sqrt{3}}{2}]$．

    查看答案和解析>>

    同步练习册答案