

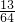
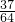
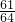
 =
=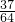


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年青岛市质检二理) (12分) 一个均匀的正四面体的四个面上分别涂有1,2,3,4四个数字,现随机投掷两次,正四面体面朝下的数字分别为![]() ,记
,记![]() .
.
(Ⅰ)分别求出![]() 取得最大值和最小值时的概率;
取得最大值和最小值时的概率;
(Ⅱ)求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)将一枚质地均匀的骰子(形状为正四面体,四个面上分别标有数字
1,2,3,4的玩具)先后抛掷两次,观察抛掷后不能看到的数字的点数依次为![]() .
.
(1)求![]() 的概率;(2)试将右侧求(1)中概率P的基本语句补充完整;(3)将a,b,3的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
的概率;(2)试将右侧求(1)中概率P的基本语句补充完整;(3)将a,b,3的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
查看答案和解析>>
科目:高中数学 来源:2014届云南省高二上学期期末考试文科数学试卷(解析版) 题型:解答题
(本题12分)一个质地均匀的正四面体的四个面上分别标示着数字1、2、3、4,一个质地均匀的骰子(正方体)的六个面上分别标示数字1、2、3、4、5、6,先后抛掷一次正四面体和骰子。
⑴列举出全部基本事件;
⑵求被压在底部的两个数字之和小于5的概率;
⑶求正四面体上被压住的数字不小于骰子上被压住的数字的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com