
分析 求出函数的定义域,将函数进行化简,然后进行求解即可.
解答 解:要使函数有意义,则$\left\{\begin{array}{l}{1-{x}^{2}≥0}\\{{x}^{2}-4x+4>0}\end{array}\right.$,
即$\left\{\begin{array}{l}{-1≤x≤1}\\{(x-2)^{2}>0}\end{array}\right.$,得$\left\{\begin{array}{l}{-1≤x≤1}\\{x≠2}\end{array}\right.$,
则-1≤x≤1,即函数的定义域为[-1,1],
此时y=$\frac{(x-2)\sqrt{1-{x}^{2}}}{\sqrt{{x}^{2}-4x+4}}$=$\frac{(x-2)\sqrt{1-{x}^{2}}}{|x-2|}$=$\frac{(x-2)\sqrt{1-{x}^{2}}}{-(x-2)}$=-$\sqrt{1-{x}^{2}}$,
∵0≤$\sqrt{1-{x}^{2}}$≤1,
∴-1≤-$\sqrt{1-{x}^{2}}$≤0,
即函数的值域为[-1,0],
故答案为:[-1,0].
点评 本题主要考查函数值域的求解,本题先求出函数的定义域,将函数进行化简是解决本题的关键.


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
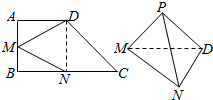 在梯形ABCD中,AD∥BC,∠ABC=90°,点M、N分别在边AB、BC上,沿直线MD、DN、NM,分别将△AMD、△CDN、△BNM折起,点A,B,C重合于一点P.
在梯形ABCD中,AD∥BC,∠ABC=90°,点M、N分别在边AB、BC上,沿直线MD、DN、NM,分别将△AMD、△CDN、△BNM折起,点A,B,C重合于一点P.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com