
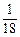 x2-
x2-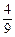 x-10与x轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动.线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)
x-10与x轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动.线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)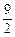 )时,△PQF的面积是否总为定值?若是,求出此定值;若不是,请说明理由;
)时,△PQF的面积是否总为定值?若是,求出此定值;若不是,请说明理由;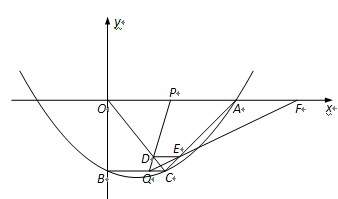
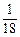 x2-
x2-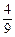 x-10中,令y=0,得x2-8x-180=0.
x-10中,令y=0,得x2-8x-180=0.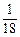 x2-
x2-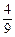 x-10中,令x=0,得y=-10.
x-10中,令x=0,得y=-10.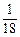 x2-
x2-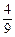 x-10得x=0或x=8.
x-10得x=0或x=8.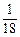 x2-
x2-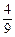 x-10=
x-10=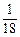 (x-4)2-
(x-4)2-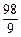
 ∴抛物线的顶点坐标为(4,-
∴抛物线的顶点坐标为(4,-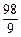 ). 4分
). 4分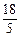 .·························································································· 6分
.·························································································· 6分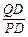 =
=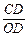 =
=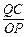 =
=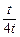 =
=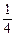 .
.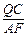 =
=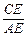 =
=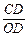 =
=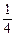 ,即
,即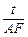 =
=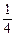 .
.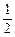 PF·OB=
PF·OB=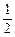 ×18×10=90
×18×10=90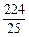 .
.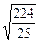 =
=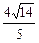 .
.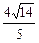 -2.··················································································· 11分
-2.··················································································· 11分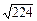 ≈15,又0≤5t≤22.5,
≈15,又0≤5t≤22.5,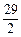 )2=
)2=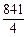 <224.
<224.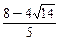 <0或t=
<0或t=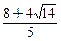 >4.5均不合题意,
>4.5均不合题意,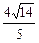 -2时,△PQF为等腰三角形.·························· 14分
-2时,△PQF为等腰三角形.·························· 14分

科目:高中数学 来源:不详 题型:解答题
 ,
, ,动点A满足|AE|=4,线段AF的垂直平分线交AE于点M。
,动点A满足|AE|=4,线段AF的垂直平分线交AE于点M。 与C1在第一象限交于点P,直线PF交抛物线于另一个点Q,求抛物线的POQ弧上的点R到直线PQ的距离的最大值。
与C1在第一象限交于点P,直线PF交抛物线于另一个点Q,求抛物线的POQ弧上的点R到直线PQ的距离的最大值。
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
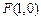 ,
,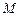 点在
点在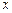 轴的负半轴上,点
轴的负半轴上,点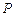 在
在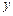 轴上,且
轴上,且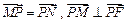 .
.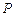 在
在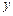 轴上运动时,求点
轴上运动时,求点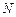 的轨迹
的轨迹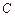 的方程;
的方程;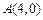 ,是否存在垂直
,是否存在垂直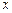 轴的直线
轴的直线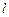 被以
被以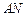 为直径的圆截得的弦长恒为定值?若存在,求出直线
为直径的圆截得的弦长恒为定值?若存在,求出直线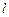 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
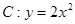 ,点A(0,-2)及点B(3,a),从点A观察点B,要使视线不被C挡住,则实数a的取值范围是
,点A(0,-2)及点B(3,a),从点A观察点B,要使视线不被C挡住,则实数a的取值范围是 | A.(-∞,10) | B.(10,+∞) | C.(-∞,4) | D.(4,+∞) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
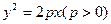 焦点为F,准线为l,经过F的直线与抛物线交于A、B两点,交准线于C点,点A在x轴上方,AK⊥l,垂足为K,若|BC|=2|BF|,且|AF|=4,则△AKF的面积是 ( )
焦点为F,准线为l,经过F的直线与抛物线交于A、B两点,交准线于C点,点A在x轴上方,AK⊥l,垂足为K,若|BC|=2|BF|,且|AF|=4,则△AKF的面积是 ( )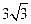 C.
C.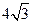 D.8
D.8查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com