练习册

  • 练习册
  • 试题
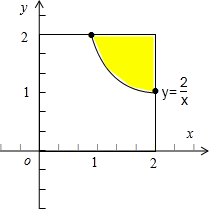    精英家教网 > 高中数学 > 题目详情
    在区间[0，2]上随机取两个数x，y，则0≤xy≤2的概率是（　　）
    A、
    1-ln2
    2
    B、
    3-2ln2
    4
    C、
    1+ln2
    2
    D、
    1+2ln2
    2
    分析：先作出图象，由题意可设两个数为x，y，则有所有的基本事件满足
    0≤x≤2
    0≤y≤2
    ，所研究的事件满足0≤y≤
    2
    x
    ，再利用图形求概率．
    解答：精英家教网解：由题意可设两个数为x，y，则所有的基本事件满足
    0≤x≤2
    0≤y≤2
    ，所研究的事件满足0≤y≤
    2
    x
    ，如图．
    总的区域是一个边长为2的正方形，它的面积是4，
    满足0≤y≤
    2
    x
    的区域的面积是4-
    ∫
    2
    1
    (2-
    2
    x
    )dx    =4-(2x-2lnx) 
    |
    2
    1
    =4-[（4-2ln2）-（2-2ln1）]=2+2ln2，
    则0≤xy≤2的概率为P=
    2+2ln2
    4
    =
    1+ln2
    2
    ，
    故选：C．
    点评：本题考查几何概率模型，求解问题的关键是能将问题转化为几何概率模型求解，熟练掌握几何概率模型的特征利于本题的转化．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：山东省聊城市2006-2007学年度高一年级第一学期期中联考　数学试题 题型：022

    探究函数f(x)＝x∈(0，＋∞)取最小值时x的值，列表如下：

    请观察表中y值随x值变化的特点，完成以下的问题：

    (1)

    函数f(x)＝(x＞0)在区间(0，2)上递减；函数f(x)＝(x＞0)在区间________上递增．当x＝________时，ymin＝________．

    (2)

    证明：函数f(x)＝(x＞0)在区间(0，2)上递减．

    查看答案和解析>>

    科目：高中数学 来源：导练必修一数学苏教版 苏教版 题型：044

    (探究题)探究函数f(x)＝x＋，x∈(0，＋∞)的最小值，并确定取得最小值时x的值，列表如下：

    ?请观察表中y值随x值变化的特点，完成以下问题：

    (1)函数f(x)＝x＋，x∈(0，＋∞)在区间(0，2)上递减；函数f(x)＝x＋，x∈(0，＋∞)在区间________上递增．当x＝________时，ymin＝________．

    (2)证明函数f(x)＝x＋，x∈(0，＋∞)在区间(0，2)上递减．

    查看答案和解析>>

    科目：高中数学 来源：河南省信阳商城高中2010－2011学年高一第一次月考数学试题 题型：044

    我们为了探究函数f(x)＝x＋，x∈(0，＋∞)的部分性质，先列表如下：

    请你观察表中y值随x值变化的特点，完成以下的问题．

    首先比较容易的看出来：此函数在区间(0，2)上是递减的；

    (1)函数f(x)＝x＋(x＞0)在区间________上递增．当x＝________时，y最小＝________．

    (2)请你根据上面性质作出此函数的大概图像；

    (3)证明：此函数在区间上(0，2)是递减的．

    查看答案和解析>>

    科目：高中数学 来源：山西省忻州一中2011－2012学年高一上学期期中考试数学试题 题型：044

    探究函数f(x)＝x＋，x∈(0，＋∞)的最小值，并确定相应的x的值，列表如下：

    请观察表中y值随x值变化的特点，完成下列问题：

    (1)若x1x2＝4，则f(x1)________f(x2)(请填写“＞，＝，＜”号)；若函数f(x)＝x＋，(x＞0)在区间(0，2)上递减，则在区间________上递增；

    (2)当x＝________时，f(x)＝x＋，(x＞0)的最小值为________；

    (3)试用定义证明f(x)＝x＋，在区间(0，2)上单调递减．

    查看答案和解析>>

    科目：高中数学 来源：0117 期中题 题型：解答题

    探究函数，x∈(0，+∞)的最小值，并确定相应的x的值，列表如下：
    请观察表中y值随x值变化的特点，完成下列问题：
    （1）若函数（x＞0）在区间(0，2)上递减，则在________上递增；
    （2）当x=________时，（x＞0）的最小值为_________；
    （3）试用定义证明（x＞0）在区间(0，2)上递减；
    （4）函数（x＜0）有最值吗？是最大值还是最小值？此时x为何值？
    解题说明：第（1）（2）两题的结果直接填写在横线上；第（4）题直接回答，不需证明。

    查看答案和解析>>

    同步练习册答案