
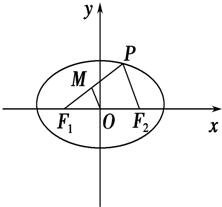
 设P为椭圆
设P为椭圆 上任意一点,F1,F2为左、右焦点.
上任意一点,F1,F2为左、右焦点. |-|
|-| |;
|; -
- =0若存在,求出P点的坐标,若不存在,试说明理由.
=0若存在,求出P点的坐标,若不存在,试说明理由. ,…(4分)
,…(4分) .…(6分)
.…(6分)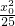 +
+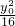 =1.①
=1.①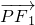 =(-3-x0,-y0),
=(-3-x0,-y0),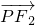 =(-3-x0,-y0),
=(-3-x0,-y0),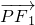 •
•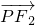 =0,∴x0-9+y0=0,②
=0,∴x0-9+y0=0,②

 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源:2011-2012学年湖南师大附中高二(上)期中数学试卷(理科)(解析版) 题型:解答题
 上任意一点,F1,F2为左、右焦点.
上任意一点,F1,F2为左、右焦点. |-|
|-| |;
|; -
- =0若存在,求出P点的坐标,若不存在,试说明理由.
=0若存在,求出P点的坐标,若不存在,试说明理由.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖南师大附中高二(上)期中数学试卷(文科)(解析版) 题型:解答题
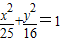 上任意一点,F1,F2为左、右焦点.
上任意一点,F1,F2为左、右焦点.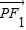 |-|
|-|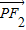 |;
|;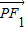 -
-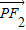 =0若存在,求出P点的坐标,若不存在,试说明理由.
=0若存在,求出P点的坐标,若不存在,试说明理由.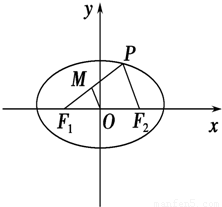
查看答案和解析>>
科目:高中数学 来源:2009-2010学年北京市朝阳区高二(上)期末数学试卷(理科)(解析版) 题型:填空题
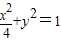 上任意一点,O为坐标原点,F为椭圆的左焦点,点M满足
上任意一点,O为坐标原点,F为椭圆的左焦点,点M满足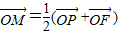 ,则
,则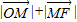 = .
= .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com