
【题目】函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ< ![]() )的图象与x轴相邻两个交点间的距离为
)的图象与x轴相邻两个交点间的距离为 ![]() ,且图象上一个最低点为M(
,且图象上一个最低点为M( ![]() ,﹣2). (Ⅰ)求f(x)的解析式;
,﹣2). (Ⅰ)求f(x)的解析式;
(Ⅱ)求f(x)的单调递增区间;
(Ⅲ)当x∈[ ![]() ,
, ![]() ]时,求f(x)的值域.
]时,求f(x)的值域.
【答案】解:(Ⅰ)由图象与x轴相邻两个交点间的距离为 ![]() ,
, ![]() =
= ![]() =
= ![]() ,∴ω=2,
,∴ω=2,
再根据图象上一个最低点为M( ![]() ,﹣2),可得A=2,2×
,﹣2),可得A=2,2× ![]() +φ=
+φ= ![]() ,φ=
,φ= ![]() ,
,
∴f(x)=2sin(2x+ ![]() ).
).
(Ⅱ)令2kπ﹣ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,求得kπ﹣
,求得kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,k∈Z;
,k∈Z;
(Ⅲ)当x∈[ ![]() ,
, ![]() ]时,
]时, ![]() ≤2x+
≤2x+ ![]() ≤
≤ ![]() ,∴sin(2x+
,∴sin(2x+ ![]() )∈[﹣1,2],故函数的值域为[﹣1,2]
)∈[﹣1,2],故函数的值域为[﹣1,2]
【解析】(Ⅰ)由周期求得ω,由最低点的坐标结合五点法作图求得A及φ的值,可得函数f(x)的解析式.(Ⅱ)由条件利用正弦函数的单调性,求得f(x)的单调递增区间.(Ⅲ)当x∈[ ![]() ,
, ![]() ],利用正弦函数的定义域和值域,求得f(x)的值域.
],利用正弦函数的定义域和值域,求得f(x)的值域.


科目:高中数学 来源: 题型:
【题目】如图是某工厂对一批新产品长度(单位:mm)检测结果的频率分布直方图.估计这批产品的中位数为( ) 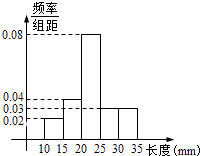
A.20
B.25
C.22.5
D.22.75
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)若cos ![]() =
= ![]() ,
, ![]() π<x<
π<x< ![]() π,求
π,求 ![]() 的值. 【答案】解:由
的值. 【答案】解:由 ![]() π<x<
π<x< ![]() π,得
π,得 ![]() π<x+
π<x+ ![]() <2π,
<2π,
又cos ![]() =
= ![]() ,∴sin
,∴sin ![]() =﹣
=﹣ ![]() ;
;
∴cosx=cos ![]() =cos
=cos ![]() cos
cos ![]() +sin
+sin ![]() sin
sin ![]() =﹣
=﹣ ![]() ,
,
从而sinx=﹣ ![]() ,tanx=7;
,tanx=7;
故原式= ![]() ;
;
(1)已知函数f(x)=2 ![]() sinxcosx+2cos2x﹣1(x∈R),若f(x0)=
sinxcosx+2cos2x﹣1(x∈R),若f(x0)= ![]() ,x0∈[
,x0∈[ ![]() ,
, ![]() ],求cos2x0的值.
],求cos2x0的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近几年,由于环境的污染,雾霾越来越严重,某环保公司销售一种PM2.5颗粒物防护口罩深受市民欢迎.已知这种口罩的进价为40元,经销过程中测出年销售量y(万件)与销售单价x(元)存在如图所示的一次函数关系,每年销售这种口罩的总开支z(万元)(不含进价)与年销量y(万件)存在函数关系z=10y+42.5. 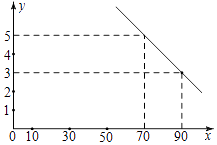
(I)求y关于x的函数关系;
(II)写出该公司销售这种口罩年获利W(万元)关于销售单价x(元)的函数关系式
(年获利=年销售总金额﹣年销售口罩的总进价﹣年总开支金额);当销售单价x为何值时,年获利最大?最大获利是多少?
(III)若公司希望该口罩一年的销售获利不低于57.5万元,则该公司这种口罩的销售单价应定在什么范围?在此条件下要使口罩的销售量最大,你认为销售单价应定为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,A,B,C三点满足 ![]() =
= ![]() +
+ ![]() . (Ⅰ)求证:A,B,C三点共线;
. (Ⅰ)求证:A,B,C三点共线;
(Ⅱ)已知A(1,cosx),B(1+sinx,cosx),x∈[0, ![]() ],f(x)=
],f(x)= ![]()
![]() ﹣(2m2+
﹣(2m2+ ![]() )|
)| ![]() |的最小值为
|的最小值为 ![]() ,求实数m的值.
,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥S﹣ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2 ![]() ,M为AB的中点.
,M为AB的中点. 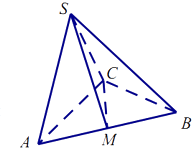
(1)求证:AC⊥SB;
(2)求二面角S﹣CM﹣A的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,所有棱长均为2,O是底面正方形ABCD中心,E为PC中点,则直线OE与直线PD所成角为( ) 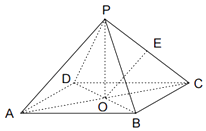
A.30°
B.60°
C.45°
D.90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com